Mapping the Earth
+8
Dan-cer
TG123
Hauchfer
outerworlds44
leotruther
k4t
Safesteef
RedorBlue
12 posters
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: Reference Materials, eBooks, Articles, Videos, Maps
Page 4 of 5
Page 4 of 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 Re: Mapping the Earth
Re: Mapping the Earth
Here is a link that should be of interest to you bdhfe
http://www.cromleck-de-rennes.com/images/cassini.jpg
It's the meridian surveyed across France begun 1683. Giovanni Cassini was tasked with this survey by the Paris Academie des Sciences in order to ascertain the shape of earth .
Cassini himself was not a follower of the Copernican model or Newton's theory of gravity but adhered to the Brahe model. Being the premier scientist/surveyor of the day he was given this task.
The reasoning for the survey was this.
If the theory of Newtonian gravity was correct then earth would be found to flatten at the poles and bulge at the equator ,i.e degrees of latitude would lengthen northwards along the meridian.
Copernicus adherents viewed the earth as a sphere, the prediction being that all degrees of latitude would be equal along any line of meridian
The survey used plane trigonometry with astronomical methods , Polaris giving the N direction and the rotating stars providing true alignment between N - S as they reached their zenith.
Cassini's survey found that from Perpignan S to Dunkirk N degrees of latitude shortened by around 1/800th Northward. So both Copernican and Newtonian models were incorrect.
His results were checked and no fault found , also backed up by other practical astronomers . Both theories were wrong. The age of "enlightenment" was brought to a halt. Huge controversy ensued .A cover up began .
Must go now but it is worth researching this if you get the time. Will add more later.
http://www.cromleck-de-rennes.com/images/cassini.jpg
It's the meridian surveyed across France begun 1683. Giovanni Cassini was tasked with this survey by the Paris Academie des Sciences in order to ascertain the shape of earth .
Cassini himself was not a follower of the Copernican model or Newton's theory of gravity but adhered to the Brahe model. Being the premier scientist/surveyor of the day he was given this task.
The reasoning for the survey was this.
If the theory of Newtonian gravity was correct then earth would be found to flatten at the poles and bulge at the equator ,i.e degrees of latitude would lengthen northwards along the meridian.
Copernicus adherents viewed the earth as a sphere, the prediction being that all degrees of latitude would be equal along any line of meridian
The survey used plane trigonometry with astronomical methods , Polaris giving the N direction and the rotating stars providing true alignment between N - S as they reached their zenith.
Cassini's survey found that from Perpignan S to Dunkirk N degrees of latitude shortened by around 1/800th Northward. So both Copernican and Newtonian models were incorrect.
His results were checked and no fault found , also backed up by other practical astronomers . Both theories were wrong. The age of "enlightenment" was brought to a halt. Huge controversy ensued .A cover up began .
Must go now but it is worth researching this if you get the time. Will add more later.
TyrannicalSawdustRex- Posts : 79
Points : 640
Reputation : 1
Join date : 2023-01-14
 Re: Mapping the Earth
Re: Mapping the Earth
TyrannicalSawdustRex wrote:Here is a link that should be of interest to you bdhfe
http://www.cromleck-de-rennes.com/images/cassini.jpg
It's the meridian surveyed across France begun 1683. Giovanni Cassini was tasked with this survey by the Paris Academie des Sciences in order to ascertain the shape of earth .
Cassini himself was not a follower of the Copernican model or Newton's theory of gravity but adhered to the Brahe model. Being the premier scientist/surveyor of the day he was given this task.
The reasoning for the survey was this.
If the theory of Newtonian gravity was correct then earth would be found to flatten at the poles and bulge at the equator ,i.e degrees of latitude would lengthen northwards along the meridian.
Copernicus adherents viewed the earth as a sphere, the prediction being that all degrees of latitude would be equal along any line of meridian
The survey used plane trigonometry with astronomical methods , Polaris giving the N direction and the rotating stars providing true alignment between N - S as they reached their zenith.
Cassini's survey found that from Perpignan S to Dunkirk N degrees of latitude shortened by around 1/800th Northward. So both Copernican and Newtonian models were incorrect.
His results were checked and no fault found , also backed up by other practical astronomers . Both theories were wrong. The age of "enlightenment" was brought to a halt. Huge controversy ensued .A cover up began .
Must go now but it is worth researching this if you get the time. Will add more later.
TyrannicalSawdustRex,
Thank you for the very interesting information.
Regarding the latitude shortening when proceeding North along the Paris meridian, it would be good to know if Cassini was using Globe-based methods for calculating latitude or not.
BDH
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
bdhfe wrote:
Dip and Refraction and Parallax
These variables come into play as a result of adjusting for distances to stars and altitudes.
There is a good explainer on these here:
http://www.siranah.de/html/sail040h.htm
As these variables are used, based on the belief of a globe earth and large distances to the stars, there is then brought into play a Nautical Almanac, of which I have the gravest suspicions. I believe the devil is in the details in this, as the Almanac is used to to Adjust what we are actually seeing to what they want us to see. IMO.
Following up on my comments regarding the Sextant and the variables added to adjust the calculation based on the Globe theory, let me say that these variables, for the most part, are based on Theory and not Experience. Thus they should be eliminated from the picture if we are to arrive at a mapping based completely on provable constants and variations.
The Altitude (Dip) variable is used because we are using the horizon with the Sextant. This would be a valid variable to use. However, the method described in this Subject does not need the use of an Altitude (Dip) adjustment... All that is done to accomplish the horizon in the method I proposed is to make the surface across which the sun's shadow is moving.... Level...
Second, the Parallax..... guess what theory needs Parallax?
Third, Refraction.... Again, what theory needs Refraction?
Perhaps, one can still use the Sextant to calculate Lat and Long, keeping its use in line with the method laid out in this Subject.
All we need to do is remove the variable for Altitude (Dip).
This can be done by employing the Bubble Sextant, which instrument creates an Artificial Horizon that uses Water, which Water always seeks its LEVEL. Hence, the use of Dip is eliminated.
Bubble Sextant, or Octant described here:
https://en.wikipedia.org/wiki/Bubble_octant
Okay, questions to be answered moving forward if one is to use a Sextant:
1. We need True North to give us Latitude. How will the Sextant provide us True North and subsequently Latitude?
2. Once our Meridian is found, how does the Sextant give us Longitude?
BDH
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
Basically, we can all use devices that help to determine the true distances. I have no closer knowledge in surveying, but even without this knowledge I can imagine that it is at least possible to determine approximate values. For example in Australia.
The individual distances of national roads can be checked, even if they are not dead straight.
1. north-south >Darwin - Adelaide
2. west-east >Perth - Sydney
These two lines can be checked by auto-mileage, at least roughly.
The biggest discrepancy between the Gleason map and globe maps is in proportion.
Is Australia as elongated as in Gleason, or does it have the proportions as in the globe maps? That should be possible to find out by auto-mileage + interpolation alone.
To what extent a sextant is infallible here I cannot judge, but the more different methods are used, the more clearly we can see which shape is the real one. In fact, since my occupation with FE, it is the shape of Australia that has struck me most. There it seems to me to be easiest to check the proportions in the Gleason map. What is then still missing is the exact position on longitude and latitude. Or in other words:
Only we can determine the actual form of Australia, and this is still shiftable, as long as we have difficulties with the determination of the absolute position.
The individual distances of national roads can be checked, even if they are not dead straight.
1. north-south >Darwin - Adelaide
2. west-east >Perth - Sydney
These two lines can be checked by auto-mileage, at least roughly.
The biggest discrepancy between the Gleason map and globe maps is in proportion.
Is Australia as elongated as in Gleason, or does it have the proportions as in the globe maps? That should be possible to find out by auto-mileage + interpolation alone.
To what extent a sextant is infallible here I cannot judge, but the more different methods are used, the more clearly we can see which shape is the real one. In fact, since my occupation with FE, it is the shape of Australia that has struck me most. There it seems to me to be easiest to check the proportions in the Gleason map. What is then still missing is the exact position on longitude and latitude. Or in other words:
Only we can determine the actual form of Australia, and this is still shiftable, as long as we have difficulties with the determination of the absolute position.

Dan-cer- Posts : 39
Points : 1382
Reputation : 0
Join date : 2020-11-28
Location : Germany
 Re: Mapping the Earth
Re: Mapping the Earth
Dan-cer wrote:Basically, we can all use devices that help to determine the true distances. I have no closer knowledge in surveying, but even without this knowledge I can imagine that it is at least possible to determine approximate values. For example in Australia.
The individual distances of national roads can be checked, even if they are not dead straight.
1. north-south >Darwin - Adelaide
2. west-east >Perth - Sydney
These two lines can be checked by auto-mileage, at least roughly.
Dan-cer,
I completely agree with you on the use of road distance and any other method that is proved by EXPERIENCE and not theory.
Dan-cer wrote:The biggest discrepancy between the Gleason map and globe maps is in proportion.
Is Australia as elongated as in Gleason, or does it have the proportions as in the globe maps? That should be possible to find out by auto-mileage + interpolation alone.
To what extent a sextant is infallible here I cannot judge, but the more different methods are used, the more clearly we can see which shape is the real one. In fact, since my occupation with FE, it is the shape of Australia that has struck me most. There it seems to me to be easiest to check the proportions in the Gleason map. What is then still missing is the exact position on longitude and latitude. Or in other words:
Only we can determine the actual form of Australia, and this is still shiftable, as long as we have difficulties with the determination of the absolute position.
Regarding Australia, here are a few maps that provide different proportioning.
Here is Gleason's Australia:

One from Maphill:

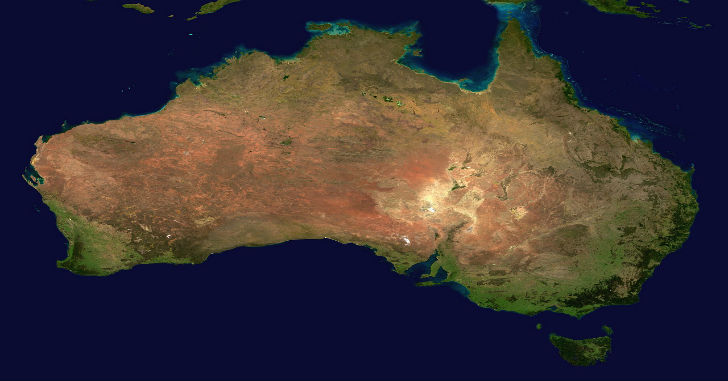
Another composite "satellite" map:
And then there is Google's etal:
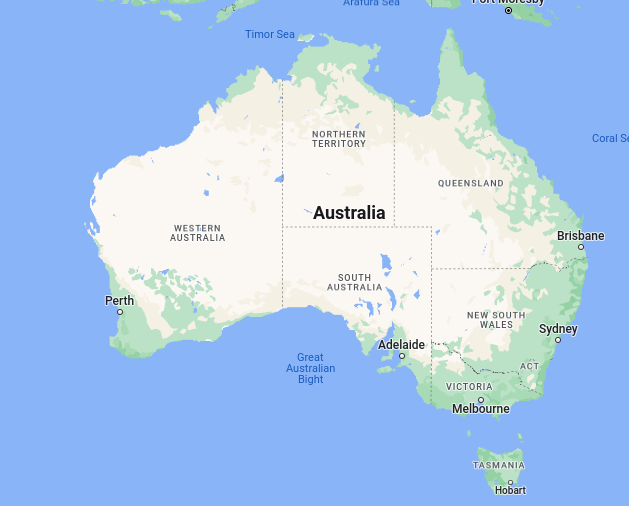
Looking at each of these maps, I believe, based on expanding lines of Longitude as one proceeds South, that the closest match to reality is the composite "satellite" map.
Let me illustrate.
Using the Longitudes provided by the Globe-nauts, running some lines from North to South from same Longitude valued cities in and north of, and in the south of Australia, the map is shown as such:
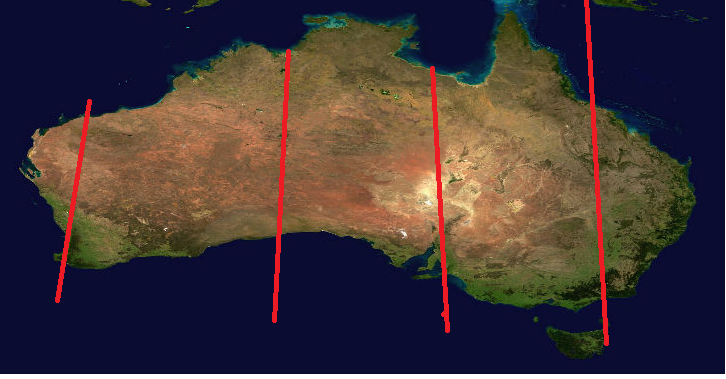
Now, granted, the lines I have drawn are based on values provided from the Wikipedia pages of those cities I chose as having the same Longitudes, but the point is this: The composite "satellite" map does show expanding longitudinal lines as one goes further South. This necessarily implies that this composite map is more real than the others that show Longitudes that are totally vertical.
The next step is to figure the distance between degrees of Longitude in the north of Australia and compare them with the distance between degrees of Longitude in the south of Australia.
Certainly places like this will aid us in our work: Eyre Highway: the Longest Straight Road in Australia
https://unusualplaces.org/eyre-highway-the-longest-straight-road-in-australia/
To be continued.
BDH
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
TyrannicalSawdustRex likes this post
 Re: Mapping the Earth
Re: Mapping the Earth
bdhfe wrote:[q
Cassini's survey found that from Perpignan S to Dunkirk N degrees of latitude shortened by around 1/800th Northward. So both Copernican and Newtonian models were incorrect.
His results were checked and no fault found , also backed up by other practical astronomers . Both theories were wrong. The age of "enlightenment" was brought to a halt. Huge controversy ensued .A cover up began .
Must go now but it is worth researching this if you get the time. Will add more later.
TyrannicalSawdustRex,
Thank you for the very interesting information.
Regarding the latitude shortening when proceeding North along the Paris meridian, it would be good to know if Cassini was using Globe-based methods for calculating latitude or not.
BDH[/quote]
There were no globe calculations at that time. Triangulation survey along the meridian would pick up the shape of earth determined by any change in length of degree of latitude. A scientific survey without bias.
The main instrument used was the transit scope which when aligned with the Pole star would only traverse along the line of meridian upon which it stood i.e. North to South . It could also give star positions as they reached zenith when aligned vertically from the same position . That allowed the line of longitude to be followed accurately as the survey continued in either direction along the meridian.
Sun position was irrelevant since clocks of the time were not accurate plus the conditions during night were more relevant since the stars provided a means of constant check.
Geovanni Cassini died in 1712 and globe calculations were later devised to map plane triangulation survey on any sized globe one required.
My view is that the original results showed the world the world to be flat and the pole star within a measurable distance although I don't rule out that our plane could also part of a much larger globe.
Basically real science based on experiment and observation was usurped by theoretic claptrap from that point on.
TyrannicalSawdustRex- Posts : 79
Points : 640
Reputation : 1
Join date : 2023-01-14
 Re: Mapping the Earth
Re: Mapping the Earth
In this video XANDREWX shows that australia is about 5000Km by length he starts the calculations at 22:40 in the video:
pitagoras- Posts : 37
Points : 687
Reputation : 0
Join date : 2022-10-22
Ricend likes this post
 Re: Mapping the Earth
Re: Mapping the Earth
pitagoras,
Thanks for the video link. I have seen his presentation and he makes a compelling case for the accuracy of the Gleason map.
However, there are some issues that need to be overcome having to do with the Gleason map.
Let me explain.
Gleason's patent application admits of EXTORSION in the map. What kind of extorsion?
Gleason states: " The extorsion of the map from that of a globe consists, mainly in the straightening out of the meridian lines allowing each to retain their original value from Greenwich, the equator to the two poles. " In other words, Gleason's calculations of Latitude and Longitude come from Greenwich, which organization uses a Globe to calculate Latitude and Longitude. All of their data is based on the Mercator projection and uses globular math formulas to arrive at the values used for locations all over the world. In the South this has created havoc for sea travel, and I dare say for land travel as well.
I posted a link to a great reference describing how Greenwich uses the system of coordinates devised by the Royal Observatory based on the Globe. And this includes Latitude and Longitude. This information is found in "The Greenwich Meridian" by Malin and Stott:
https://www.amazon.com/gp/product/0319000389/ref=dbs_a_def_rwt_hsch_vapi_taft_p1_i0
From an earlier post I made on this forum:
Quoting a Reverend Thomas Milner,: “In the southern hemisphere, navigators to India have often fancied themselves east of the Cape when still west, and have been driven ashore on the African coast, which, according to their reckoning, lay behind them."
This information describes an issue of navigation South of the equator. The navigators, going by data (likely originating from Greenwich) put the navigators further East than where they were actually located. If the data said they were at 30 degrees East Longitude when in fact they were more like 15 degrees East Longitude, the charts were wrong and they were wrong by the calculation of LONGITUDE calculated by the Globe theory. 15 degrees versus 30 degrees is a large difference!!
As well, the calculations used for Latitude, based on the Globe data, can be called into question.
For example: a post above from TyrannicalSawdustRex describes Giovanni Cassini's findings in 1683 for the changes in Latitude discovered when surveying for the shape of the Earth.
One other thing I would like to say with regard to Latitude as well. The real world, since it is a flat plane stretching out from a center point to the Southern climes, is not a globe with two poles. Those that believe that the Earth is a globe must believe that the Earth has two poles -- the North and the South. As such, they must conform the shape and distances of land masses to arrive at a globe. It is likely then that there is a stretching or shrinking of said land masses to make their pretty ball world.
Hence, the very erroneous data used by Greenwich in dealing with everything South of the equator.
One more thing about the actual size of Australia: Air flight times from Brisbane in the East and Perth in the West are between 4.5 and 5.5 hours.
Air flight times between Los Angeles and New York City average between 5.25 and 6.5 hours. This is indicative of a greater distance being traveled from LA to NY, the distance being 2450 miles. So, how big is Australia?
bdh
Thanks for the video link. I have seen his presentation and he makes a compelling case for the accuracy of the Gleason map.
However, there are some issues that need to be overcome having to do with the Gleason map.
Let me explain.
Gleason's patent application admits of EXTORSION in the map. What kind of extorsion?
Gleason states: " The extorsion of the map from that of a globe consists, mainly in the straightening out of the meridian lines allowing each to retain their original value from Greenwich, the equator to the two poles. " In other words, Gleason's calculations of Latitude and Longitude come from Greenwich, which organization uses a Globe to calculate Latitude and Longitude. All of their data is based on the Mercator projection and uses globular math formulas to arrive at the values used for locations all over the world. In the South this has created havoc for sea travel, and I dare say for land travel as well.
I posted a link to a great reference describing how Greenwich uses the system of coordinates devised by the Royal Observatory based on the Globe. And this includes Latitude and Longitude. This information is found in "The Greenwich Meridian" by Malin and Stott:
https://www.amazon.com/gp/product/0319000389/ref=dbs_a_def_rwt_hsch_vapi_taft_p1_i0
From an earlier post I made on this forum:
Quoting a Reverend Thomas Milner,: “In the southern hemisphere, navigators to India have often fancied themselves east of the Cape when still west, and have been driven ashore on the African coast, which, according to their reckoning, lay behind them."
This information describes an issue of navigation South of the equator. The navigators, going by data (likely originating from Greenwich) put the navigators further East than where they were actually located. If the data said they were at 30 degrees East Longitude when in fact they were more like 15 degrees East Longitude, the charts were wrong and they were wrong by the calculation of LONGITUDE calculated by the Globe theory. 15 degrees versus 30 degrees is a large difference!!
As well, the calculations used for Latitude, based on the Globe data, can be called into question.
For example: a post above from TyrannicalSawdustRex describes Giovanni Cassini's findings in 1683 for the changes in Latitude discovered when surveying for the shape of the Earth.
One other thing I would like to say with regard to Latitude as well. The real world, since it is a flat plane stretching out from a center point to the Southern climes, is not a globe with two poles. Those that believe that the Earth is a globe must believe that the Earth has two poles -- the North and the South. As such, they must conform the shape and distances of land masses to arrive at a globe. It is likely then that there is a stretching or shrinking of said land masses to make their pretty ball world.
Hence, the very erroneous data used by Greenwich in dealing with everything South of the equator.
One more thing about the actual size of Australia: Air flight times from Brisbane in the East and Perth in the West are between 4.5 and 5.5 hours.
Air flight times between Los Angeles and New York City average between 5.25 and 6.5 hours. This is indicative of a greater distance being traveled from LA to NY, the distance being 2450 miles. So, how big is Australia?
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
Dan-cer and TyrannicalSawdustRex like this post
 Re: Mapping the Earth
Re: Mapping the Earth
@ bdhfe
A great idea. Unfortunately, these measurements have become impossible here in Germany.
The sky here is 99% in a color that can only be called depression gray...
With a large amount of measurement results, your world map will have a strong resemblance to Alexander Gleason's map.
@ pitagoras
This is an interesting video from XANDREWX, even if the calculation method is a little unconventional.
My calculation is only slightly different and unconventional too..
He comes to 5219 km; my calculation is 5263 km.
I also see the elongated shape of Australia on Gleoson's map as the true shape.
In my opinion, what speaks in favor of the Gleason Map is the following:
All the coordinates are right there that every other map and even the globe uses.
(I hate using that ugly thing as a reference...)
All navigation devices use this coordinate system and find the destination reliably.
All locations are on the exact longitude where the sun reaches its highest point at noon.
In the Merkator projection, north points vertically upwards.
If these meridians meet at the North Pole, the position of the continents must inevitably be arranged as Alex Gleason did.
We are not shown the North Pole anyway; there is still enough room for rumors...
Why else would the map be in the UN logo?
The Roman reed symbolizes the area of power and imitates the edge of the ice.
I have been fascinated by the Gleason Map since I first saw it and was looking for a method to calculate distances...
The result is an Excel spreadsheet that allows you to calculate distances on the Gleason Map using coordinates.
With all official distance calculators, the ridiculous curvature of the earth is also calculated.
In this stupid theory, the 90 degree distance from the North Pole to the equator would be a quarter circle whose radius corresponds to the circumference of the equator.
This distance would be 5400 nautical miles on any conventional calculator.
(6214.212 miles or 10000.80 km)
This is WRONG.
When Alex Gleason created his map, he used all the data available to him at the time. What else could he have done?
At the top left of his map it says:
"Longitude and Time Calculator"
And his patent refers exactly to this.
The fact that he created an outstanding world map in the process was certainly no accident...
This is where I start with my calculation method:
The definition of the nautical mile was based on the path of the sun over the equator at the equinoxes.
1 nautical mile is equal to 1 minute of arc.
(The sun needs four minutes to travel this distance, resulting in 15 degrees for one hour.)
60 arc minutes are 1 degree (60 nautical miles)
60 nautical miles × 360 degrees = 21600 nautical miles as the circumference of the equator.
Converted, this is 24,856.836 miles or 40003.200 km.
On the flat Earth, the RADIUS of the equator is the distance from the North Pole to the equator.
That is 3437.747 nautical miles (3956.088 miles or 6366.707 km)
The following values result for the distance along the longitudes for one degree:
3437.747 nautical miles (radius) ÷ 90° = 38.197 miles
3956.088 miles ÷ 90° = 43.956 miles
6366.707 km ÷ 90° = 70.741 km
With my spreadsheet you only have to enter the coordinates of two points and the distance is displayed immediately.
The short video (no audio) shows my table with the calculation of the distance of the two airports Perth and Sydney.
5263 km or 3270 miles fit very well to the elongated shape of Australia.
https://www.youtube.com/watch?v=1pVdG7hRVzs
The spreadsheet can be downloaded from my Google Drive folder.
https://drive.google.com/drive/folders/1TloiUPaKlGP4jPYsFCnLwlWBAWalUJzW
I am well aware that the results are very different from the spherical calculations.
If you spin this out further, the smaller distance values result in speeds of approx. 600 instead of 900 kilometers per hour for passenger airplanes, for example; but that's still pretty fast for a flying bus...
If you look at the aerodynamics of the SR-71, which reaches around 2100 mph, the lower passenger airplanes speeds sound very logical.
Eddie Alencar's book "16 Emergency Landings Proving Flat Earth" deals with the jet streams, which causes a much shorter flight time for some flights. (Chapter 14)
The pilots know about this and use it to make faster progress.
A great idea. Unfortunately, these measurements have become impossible here in Germany.
The sky here is 99% in a color that can only be called depression gray...
With a large amount of measurement results, your world map will have a strong resemblance to Alexander Gleason's map.
@ pitagoras
This is an interesting video from XANDREWX, even if the calculation method is a little unconventional.
My calculation is only slightly different and unconventional too..
He comes to 5219 km; my calculation is 5263 km.
I also see the elongated shape of Australia on Gleoson's map as the true shape.
In my opinion, what speaks in favor of the Gleason Map is the following:
All the coordinates are right there that every other map and even the globe uses.
(I hate using that ugly thing as a reference...)
All navigation devices use this coordinate system and find the destination reliably.
All locations are on the exact longitude where the sun reaches its highest point at noon.
In the Merkator projection, north points vertically upwards.
If these meridians meet at the North Pole, the position of the continents must inevitably be arranged as Alex Gleason did.
We are not shown the North Pole anyway; there is still enough room for rumors...
Why else would the map be in the UN logo?
The Roman reed symbolizes the area of power and imitates the edge of the ice.
I have been fascinated by the Gleason Map since I first saw it and was looking for a method to calculate distances...
The result is an Excel spreadsheet that allows you to calculate distances on the Gleason Map using coordinates.
With all official distance calculators, the ridiculous curvature of the earth is also calculated.
In this stupid theory, the 90 degree distance from the North Pole to the equator would be a quarter circle whose radius corresponds to the circumference of the equator.
This distance would be 5400 nautical miles on any conventional calculator.
(6214.212 miles or 10000.80 km)
This is WRONG.
When Alex Gleason created his map, he used all the data available to him at the time. What else could he have done?
At the top left of his map it says:
"Longitude and Time Calculator"
And his patent refers exactly to this.
The fact that he created an outstanding world map in the process was certainly no accident...
This is where I start with my calculation method:
The definition of the nautical mile was based on the path of the sun over the equator at the equinoxes.
1 nautical mile is equal to 1 minute of arc.
(The sun needs four minutes to travel this distance, resulting in 15 degrees for one hour.)
60 arc minutes are 1 degree (60 nautical miles)
60 nautical miles × 360 degrees = 21600 nautical miles as the circumference of the equator.
Converted, this is 24,856.836 miles or 40003.200 km.
On the flat Earth, the RADIUS of the equator is the distance from the North Pole to the equator.
That is 3437.747 nautical miles (3956.088 miles or 6366.707 km)
The following values result for the distance along the longitudes for one degree:
3437.747 nautical miles (radius) ÷ 90° = 38.197 miles
3956.088 miles ÷ 90° = 43.956 miles
6366.707 km ÷ 90° = 70.741 km
With my spreadsheet you only have to enter the coordinates of two points and the distance is displayed immediately.
The short video (no audio) shows my table with the calculation of the distance of the two airports Perth and Sydney.
5263 km or 3270 miles fit very well to the elongated shape of Australia.
https://www.youtube.com/watch?v=1pVdG7hRVzs
The spreadsheet can be downloaded from my Google Drive folder.
https://drive.google.com/drive/folders/1TloiUPaKlGP4jPYsFCnLwlWBAWalUJzW
I am well aware that the results are very different from the spherical calculations.
If you spin this out further, the smaller distance values result in speeds of approx. 600 instead of 900 kilometers per hour for passenger airplanes, for example; but that's still pretty fast for a flying bus...
If you look at the aerodynamics of the SR-71, which reaches around 2100 mph, the lower passenger airplanes speeds sound very logical.
Eddie Alencar's book "16 Emergency Landings Proving Flat Earth" deals with the jet streams, which causes a much shorter flight time for some flights. (Chapter 14)
The pilots know about this and use it to make faster progress.

johannes.wallenfang- Posts : 13
Points : 262
Reputation : 0
Join date : 2023-11-23
Age : 60
Location : Germany
Safesteef likes this post
 Re: Mapping the Earth
Re: Mapping the Earth
johannes.wallenfang wrote:@ bdhfe
A great idea. Unfortunately, these measurements have become impossible here in Germany.
The sky here is 99% in a color that can only be called depression gray...
With a large amount of measurement results, your world map will have a strong resemblance to Alexander Gleason's map.
johannes,
I am sorry to hear that about Germany. Perhaps, once a sufficient amount of lat/longs taken in neighboring countries is completed, the outline of Germany will appear?
Secondly, a large amount of measurements will present a world map that most certainly bears a strong resemblance to Gleason's..... North of the Equator.
As for South of the equator, there will be big differences the further one travels south.
See the following testimonials from navigators in the southern climes:
"During Captain James Clark Ross’s voyages around the Antarctic circumference, he often wrote in his journal perplexed at how they routinely found themselves out of accordance with their charts, stating that they found themselves an average of 12-16 miles outside their reckoning every day, later on further south as much as 29 miles. "
" Lieutenant Charles Wilkes commanded a United States Navy exploration expedition to the Antarctic from 1838 to 1842, and in his journals also mentioned being consistently east of his reckoning, sometimes over 20 miles in less than 18 hours. "
" To quote Reverend Thomas Milner, “In the southern hemisphere, navigators to India have often fancied themselves east of the Cape when still west, and have been driven ashore on the African coast, which, according to their reckoning, lay behind them. This misfortune happened to a fine frigate, the Challenger, in 1845. How came Her Majesty’s Ship ‘Conqueror,’ to be lost? How have so many other noble vessels, perfectly sound, perfectly manned, perfectly navigated, been wrecked in calm weather, not only in dark night, or in a fog, but in broad daylight and sunshine – in the former case upon the coasts, in the latter, upon sunken rocks – from being ‘out of reckoning?’ "
"In the ball-Earth model Antarctica is an ice continent which covers the bottom of the ball from 78 degrees South latitude to 90 and is therefore not more than 12,000 miles in circumference. Many early explorers including Captain Cook and James Clark Ross, however, in attempting Antarctic circumnavigation took 3 to 4 years and clocked 50-60,000 miles around. The British ship Challenger also made an indirect but complete circumnavigation of Antarctica traversing 69,000 miles. This is entirely inconsistent with the ball model. "
Above quotes taken from: Flat Earth Proofs Part 1
Now, why the big differences in distance and location experienced by these navigators' testimonies when traveling in the South?
Because, they were using charts derived from the Royal Observatory's calculations based on a globe model.
The globe model necessitates that the distance between lines of longitude decrease as one moves south toward the South Pole. The flat earth model necessitates that the distance between lines of longitude increase as one moves south towards the Southern Ice Wall.
Hence, any distances provided by the charts based on the globe model, in the southern climes, will be incorrect.
Likewise, the Latitude and Longitude calculations in the South are incorrect since these are based on Greenwich data calculations.
To correct this situation, the practical methods of deriving Latitude and Longitude at your meridian can be employed for this purpose, except for in Germany that is.
By the way, I love your Excel spreadsheet!! It is fantastic. The only issue I have with it are the Latitude and Longitude values used. I am guessing that they are based on the globe theory??
And secondly, as there is a distance variation between lines of Longitude at different Latitudes, are these taken into account with the distances between locations? Or do they need to be?
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
Adding to what I just posted, as an illustration to show why the Greenwich Lats and Longs are incorrect in the southern climes, here is some information and data.
1. From Flat Earth Proofs Part 1:
Practical distance measurements taken from “The Australian Handbook, Almanack, Shippers’ and Importers’ Directory” state that the straight line distance between Sydney and Nelson is 1550 statute miles. Their given difference in longitude is 22 degrees 2’14”. Therefore if 22 degrees 2’14” out of 360 is 1550 miles, the entirety would measure 25,182 miles.
2. From Wikipedia, the Longitude for Sydney Australia is 151 degrees 12 minutes 36 seconds and the Longitude for Nelson New Zealand is 173 degrees 17 minutes 2 seconds yielding a difference of 22 degrees 4 minutes 26 seconds.
So, we see a difference between the Australian Handbook data and Wikipedia regarding the Longitude. Which one is correct? It goes without saying that the Almanac is the correct one.**
Wikipedia's Lats and Longs need some work!!
Likewise, the distance provided by the site https://www.distancecalculator.net shows 1308 miles between the two cities. Again, it is likely that the Lat/Longs used there are wonky as well.
Next, using the Distance Calculator Excel spreadsheet, the DMS longitude for Nelson New Zealand is 173° 13' 15.5748" and the longitude for Sydney Australia is 151° 10' 37.2072" yielding a difference of 22 degrees 2 minutes 38.3676 seconds. This difference is much closer to the coordinates listed in the Australian Handbook above.
The distance between Nelson and Sydney from the Distance Calculator yields a value of 2168 statute miles, 1884 nautical miles, or 3490 kilometers.
However, this calculation does not match the Australian Handbook Almanak. It is 618 miles different although the longitude difference is nearly the same between the Excel spreadsheet and the Almanak. This would indicate an issue with distance between degrees of longitude. We know that as one moves south, the distance between a degree of longitude increases.
** Addendum - Correction
The Australian Handbook Almanak, since it is likely based on globe calculations, is itself suspect. It would be more accurate to say the Distance Calculator is providing the correct distance.
bdh
1. From Flat Earth Proofs Part 1:
Practical distance measurements taken from “The Australian Handbook, Almanack, Shippers’ and Importers’ Directory” state that the straight line distance between Sydney and Nelson is 1550 statute miles. Their given difference in longitude is 22 degrees 2’14”. Therefore if 22 degrees 2’14” out of 360 is 1550 miles, the entirety would measure 25,182 miles.
2. From Wikipedia, the Longitude for Sydney Australia is 151 degrees 12 minutes 36 seconds and the Longitude for Nelson New Zealand is 173 degrees 17 minutes 2 seconds yielding a difference of 22 degrees 4 minutes 26 seconds.
So, we see a difference between the Australian Handbook data and Wikipedia regarding the Longitude. Which one is correct? It goes without saying that the Almanac is the correct one.**
Wikipedia's Lats and Longs need some work!!
Likewise, the distance provided by the site https://www.distancecalculator.net shows 1308 miles between the two cities. Again, it is likely that the Lat/Longs used there are wonky as well.
Next, using the Distance Calculator Excel spreadsheet, the DMS longitude for Nelson New Zealand is 173° 13' 15.5748" and the longitude for Sydney Australia is 151° 10' 37.2072" yielding a difference of 22 degrees 2 minutes 38.3676 seconds. This difference is much closer to the coordinates listed in the Australian Handbook above.
The distance between Nelson and Sydney from the Distance Calculator yields a value of 2168 statute miles, 1884 nautical miles, or 3490 kilometers.
However, this calculation does not match the Australian Handbook Almanak. It is 618 miles different although the longitude difference is nearly the same between the Excel spreadsheet and the Almanak. This would indicate an issue with distance between degrees of longitude. We know that as one moves south, the distance between a degree of longitude increases.
** Addendum - Correction
The Australian Handbook Almanak, since it is likely based on globe calculations, is itself suspect. It would be more accurate to say the Distance Calculator is providing the correct distance.
bdh
Last edited by bdhfe on Fri Dec 22, 2023 7:07 am; edited 2 times in total
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
A bit more information on Cassini and latitude. Jean Picard triangulated one degree of lat. across Paris giving the result as 110.46km - around 68.6mls.
This result was used as the starting point in Cassini's survey to the South and North.
A few years ago I extrapolated Picard's value northwards to the pole using Cassini's measured degree of shortening of latitude towards the pole. The length of one degree latitude at the pole was around 65mls. I do have it written down somewhere.
I didn't extrapolate to the "equator" because its distance from the pole has never been triangulated.
I also presume that atmospheric refraction would also play an increasing part the further south one went and I don't know how this would affect any calculations.
I do think that the tropic of cancer is not at 23.4N . Anyone living along that line would be doing a great service if they could check that with a telescope/or sextant centred on the pole star.
Good luck with your efforts bdhfe!
This result was used as the starting point in Cassini's survey to the South and North.
A few years ago I extrapolated Picard's value northwards to the pole using Cassini's measured degree of shortening of latitude towards the pole. The length of one degree latitude at the pole was around 65mls. I do have it written down somewhere.
I didn't extrapolate to the "equator" because its distance from the pole has never been triangulated.
I also presume that atmospheric refraction would also play an increasing part the further south one went and I don't know how this would affect any calculations.
I do think that the tropic of cancer is not at 23.4N . Anyone living along that line would be doing a great service if they could check that with a telescope/or sextant centred on the pole star.
Good luck with your efforts bdhfe!
TyrannicalSawdustRex- Posts : 79
Points : 640
Reputation : 1
Join date : 2023-01-14
 Re: Mapping the Earth
Re: Mapping the Earth
TyrannicalSawdustRex,
Great information!
When we have been considering the variations in Longitude for mapping points on the Earth, I have not considered the fact that Latitude distance variation is very real.
Theoretically, the Globe model requires, or strongly suggests, an even distance around the globe from North to South. Thus the ASSUMED Latitude distances with little or no variation. One goes from 0 to 180 degrees on a ball, dividing the total distance by 180 to get the distance between degrees Latitude.
However, we are not on a ball, so this assumption fails.
Your suggestion on finding the true Tropic of Cancer would certainly help provide a Latitude variation factor, which can be incorporated into distance calculations at various locations North and South.
bdh
Great information!
When we have been considering the variations in Longitude for mapping points on the Earth, I have not considered the fact that Latitude distance variation is very real.
Theoretically, the Globe model requires, or strongly suggests, an even distance around the globe from North to South. Thus the ASSUMED Latitude distances with little or no variation. One goes from 0 to 180 degrees on a ball, dividing the total distance by 180 to get the distance between degrees Latitude.
However, we are not on a ball, so this assumption fails.
Your suggestion on finding the true Tropic of Cancer would certainly help provide a Latitude variation factor, which can be incorporated into distance calculations at various locations North and South.
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
TyrannicalSawdustRex likes this post
 Re: Mapping the Earth
Re: Mapping the Earth
johannes.wallenfang wrote:
I also see the elongated shape of Australia on Gleason's map as the true shape.
johannes,
I tend to agree with your view. The question is how accurate are the Lat/Longs.
johannes.wallenfang wrote:
In my opinion, what speaks in favor of the Gleason Map is the following:
All the coordinates are right there that every other map and even the globe uses.
(I hate using that ugly thing as a reference...)
All navigation devices use this coordinate system and find the destination reliably.
If you are referring to GPS, then you are partly correct here. There are limitations to GPS navigation by aircraft and as such the use of VOR, DME, and NDB, among others.
See https://www.flightdeckfriend.com/ask-a-pilot/how-do-commercial-aircraft-navigate/ for more details.
johannes.wallenfang wrote:
All locations are on the exact longitude where the sun reaches its highest point at noon.
For sure. Let's confirm that value for the longitude manually rather than take a greece-baller's word for it. No offence intended to Greeks.
johannes.wallenfang wrote:
Eddie Alencar's book "16 Emergency Landings Proving Flat Earth" deals with the jet streams, which causes a much shorter flight time for some flights. (Chapter 14)
The pilots know about this and use it to make faster progress.
I will take a look at it. Thanks!
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
Regarding GPS and Australia, here are a few links about GPS issues in Australia....
https://www.antarcticajournal.com/gps-not-working-in-australia/
https://www.geologyin.com/2016/09/australia-is-drifting-so-fast-gps-cant.html
https://www.atlasobscura.com/articles/australias-entire-gps-navigation-is-off-by-5-feet
https://mashable.com/article/gps-australia-investment-accuracy
https://www.cnet.com/tech/mobile/apple-maps-gets-drivers-lost-in-australian-outback-police-warn/
bdh
https://www.antarcticajournal.com/gps-not-working-in-australia/
https://www.geologyin.com/2016/09/australia-is-drifting-so-fast-gps-cant.html
https://www.atlasobscura.com/articles/australias-entire-gps-navigation-is-off-by-5-feet
https://mashable.com/article/gps-australia-investment-accuracy
https://www.cnet.com/tech/mobile/apple-maps-gets-drivers-lost-in-australian-outback-police-warn/
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
I do recall reading about a recent journey to the south pole , can't recall whose but there were some interesting details in the article .
Apparently travel on Antarctica requires the use of special handheld tracking device which provides your route and you are obliged to stick to it. Basically you are guided to where ever the barbers pole has been positioned for your visit. That's how it seems to me.
https://outdoors.stackexchange.com/questions/21454/how-do-you-know-you-have-reached-north-or-south-pole-without-gps
This site gives answers as to why GPS is not accurate and shows it is based on the theoretic geoid.
Also gives a loose mention to satellites used to triangulate at the pole - which is nonsense.
Don't see how triangulation from 3 moving objects can be carried out. I know they are supposed to be geostationary but any slight movement in any direction would throw remove accuracy.
Nice links bdh.
Apparently travel on Antarctica requires the use of special handheld tracking device which provides your route and you are obliged to stick to it. Basically you are guided to where ever the barbers pole has been positioned for your visit. That's how it seems to me.
https://outdoors.stackexchange.com/questions/21454/how-do-you-know-you-have-reached-north-or-south-pole-without-gps
This site gives answers as to why GPS is not accurate and shows it is based on the theoretic geoid.
Also gives a loose mention to satellites used to triangulate at the pole - which is nonsense.
Don't see how triangulation from 3 moving objects can be carried out. I know they are supposed to be geostationary but any slight movement in any direction would throw remove accuracy.
Nice links bdh.
TyrannicalSawdustRex- Posts : 79
Points : 640
Reputation : 1
Join date : 2023-01-14
Admin likes this post
 Re: Mapping the Earth
Re: Mapping the Earth
The following diagram comes from Alex Gleason's book "Is the Earth a Globe?"

Logic tells us that the Longitudes calculated all around the world are accurately expressed due to the shape of the flat earth.
As such is the case, no astronomer or geographer would dare provide any other value for a given location than the obvious one calculated by referencing Gleason's Time and Longitude map.
Figure 43 in the diagram above provides the variation in distance between degrees of Longitude as one moves from North to South.
As can be seen, at the equator, the distance between degrees of Longitude is 60 nautical miles. North of the equator the distance decreases to 0 miles at the Pole.
Going South, the distance increases to 120 miles at 90 degrees South Latitude.
For Latitude, there is, in broad terms, very little variation as the Latitude distance values are illustrated below: ( from this site: https://www.thoughtco.com/degree-of-latitude-and-longitude-distance-4070616

I have proved this value by the distance tests I performed in rural Washington state USA.
So, at the equator 60 miles per degree of Longitude, 69 miles per degree of Latitude.
Using these numbers in johannes' Distance Calculator provides very accurate distance values from any point I have tested thus far.
Note: I did have to adjust his Distance Calculator to use the 69 miles per degree of Latitude instead of the value arrived at by dividing 3956 by 90.
Thus far, that is, in the North. I have not tested distances at the equator yet, nor distances in the South. I know the Distance Calculator will provide accurate numbers in the South and at the Equator, and these numbers will diverge greatly from the globalist fantasy numbers.
One striking detail emerges from this testing and the use of 60 miles/degree Longitude and 69 miles/degree Latitude at the Equator.
On the flat Earth, the circumference of the Earth at the Equator is now: 36663 Statute miles around the Earth at the Equator.
AND NOT the value of 24900 statute miles arrived at by globe theorists. See here: Earth's Circumference
The 36,663 statute mile value is not based on a globe fantasy guess, but instead is based on logic and mathematics.
Even more interesting, the distance between Perth and Sydney Australia is now 4823 statute miles, based on the Lat/Long coordinates provided to us by the nut cases in Greenwich. Based on the GPS issues in Australia, we need to manually measure the latitude and longitudes in each location -- Perth and Sydney that is.
bdh

Logic tells us that the Longitudes calculated all around the world are accurately expressed due to the shape of the flat earth.
As such is the case, no astronomer or geographer would dare provide any other value for a given location than the obvious one calculated by referencing Gleason's Time and Longitude map.
Figure 43 in the diagram above provides the variation in distance between degrees of Longitude as one moves from North to South.
As can be seen, at the equator, the distance between degrees of Longitude is 60 nautical miles. North of the equator the distance decreases to 0 miles at the Pole.
Going South, the distance increases to 120 miles at 90 degrees South Latitude.
For Latitude, there is, in broad terms, very little variation as the Latitude distance values are illustrated below: ( from this site: https://www.thoughtco.com/degree-of-latitude-and-longitude-distance-4070616

I have proved this value by the distance tests I performed in rural Washington state USA.
So, at the equator 60 miles per degree of Longitude, 69 miles per degree of Latitude.
Using these numbers in johannes' Distance Calculator provides very accurate distance values from any point I have tested thus far.
Note: I did have to adjust his Distance Calculator to use the 69 miles per degree of Latitude instead of the value arrived at by dividing 3956 by 90.
Thus far, that is, in the North. I have not tested distances at the equator yet, nor distances in the South. I know the Distance Calculator will provide accurate numbers in the South and at the Equator, and these numbers will diverge greatly from the globalist fantasy numbers.
One striking detail emerges from this testing and the use of 60 miles/degree Longitude and 69 miles/degree Latitude at the Equator.
On the flat Earth, the circumference of the Earth at the Equator is now: 36663 Statute miles around the Earth at the Equator.
AND NOT the value of 24900 statute miles arrived at by globe theorists. See here: Earth's Circumference
The 36,663 statute mile value is not based on a globe fantasy guess, but instead is based on logic and mathematics.
Even more interesting, the distance between Perth and Sydney Australia is now 4823 statute miles, based on the Lat/Long coordinates provided to us by the nut cases in Greenwich. Based on the GPS issues in Australia, we need to manually measure the latitude and longitudes in each location -- Perth and Sydney that is.
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
HOW I ARRIVED AT 36663 MILES FOR THE CIRCUMFERENCE OF A CIRCLE AT THE EQUATOR
Using the j's Distance Calculator spreadsheet v5.0 I ran some tests for locations near my home.
One such test was conducted at Farmer, WA and Withrow, WA. See illustrations below:
Google Earth image of Farmer, WA to Withrow, WA. The black lines represent one mile marks. Withrow is directly NORTH of Farmer.
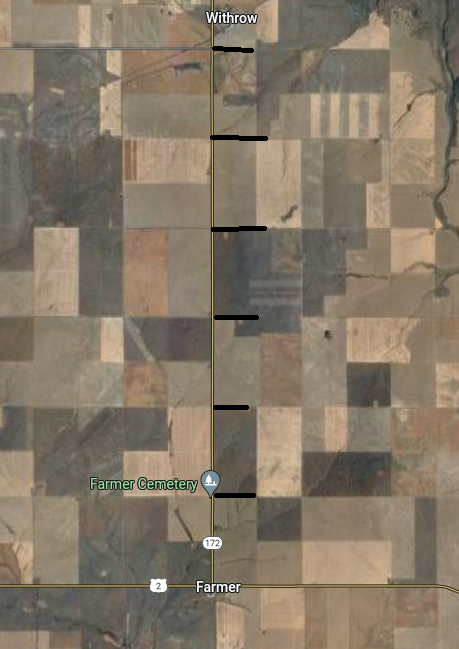
The mileage between Farmer and Withrow is 6 miles. This is proven by the mileage sign and the six one mile markers dividing each section of land between Farmer and Withrow, each Section of land equally 1 mile on a side.

The coordinates of each location are entered into j's Distance Calculator v5.0
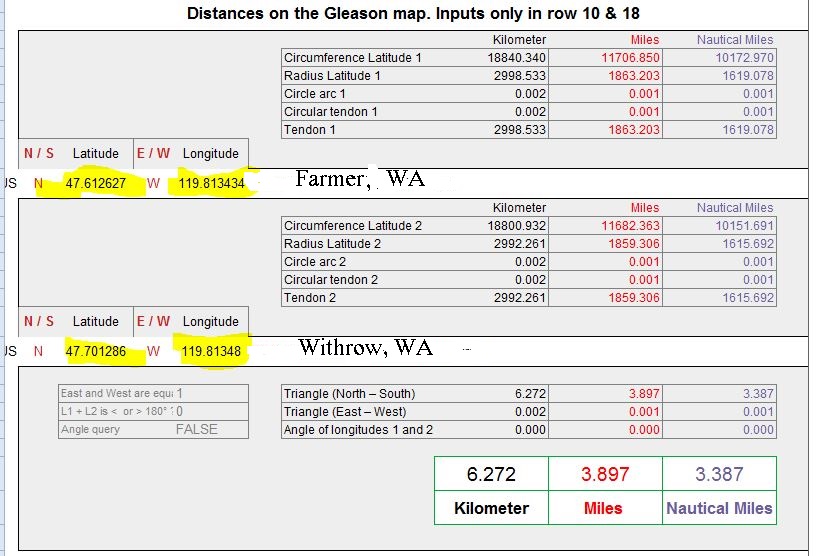
Interestingly, the Calculator provides an answer of less than 4 miles. This is 67 percent of the actual distance between Farmer and Withrow.
------------
Second example
The distance between Seattle WA and Spokane WA is 225 miles
j's Distance Calculator 5.0 provides the value of 155 miles. See below:

Again, the Calculator is providing a distance that is 68 percent of the actual distance between Spokane and Seattle.
-------------
Now why is this? j's Distance Calculator is absolutely the most valuable tool to provide accurate distances between locations anywhere in the world. And I am NOT being facetious here. Its potential is enormous.
However, there is a baseline assumption that is incorrect. johannes is basing his values on the following numbers:

The Radius value of 3956.088 miles over 90 degrees Latitude yields 44 miles per degree of Latitude.
But we know that the distance between degrees of Latitude is 68 or 69 miles, correct??
We also know that there are 90 degrees of Latitude between the Equator and the North Pole. So 90 is correct.
Hence, the value of 3956.088 miles for the Radius of the circle at the Equator is incorrect, as it yields a too small a value for distance per degree of Latitude.
The actual Radius value has to be ((100 - 67) / 67 ) * 100 = 50% larger than 3956.088.
This equates to approximately 5838 miles for the Radius.
And 5838 times 2 times PI = the Circumference of a circle at the Equator = approximately 36663 statute miles.
By plugging in this adjustment to j's Distance Calculator I now arrive at 225 miles between Seattle and Spokane, and 6 miles between Withrow and Farmer WA.
Please note that there will be a close approximation of distances, North of the Equator and especially North of the Tropic of Cancer, between the j's Distance Calculator and globe model measurements.
Secondly, of note, there will be a complete match between j's Distance Calculator and globe model measuring on all Longitudinal meridians due to the fact that there is no influence of the globe on the straight lines of Longitude. For example: Point A at Longitude X to Point B on Longitude X will have the same distance value between j's Distance Calculator and the globe model measurement.
Thirdly, of note, the differences between j's DC and globe model measurements will increase the further one travels South.
I will provide the adjustment values I changed in johannes' spreadsheet in order to correct the longitudinal issue.
bdh
Using the j's Distance Calculator spreadsheet v5.0 I ran some tests for locations near my home.
One such test was conducted at Farmer, WA and Withrow, WA. See illustrations below:
Google Earth image of Farmer, WA to Withrow, WA. The black lines represent one mile marks. Withrow is directly NORTH of Farmer.

The mileage between Farmer and Withrow is 6 miles. This is proven by the mileage sign and the six one mile markers dividing each section of land between Farmer and Withrow, each Section of land equally 1 mile on a side.

The coordinates of each location are entered into j's Distance Calculator v5.0

Interestingly, the Calculator provides an answer of less than 4 miles. This is 67 percent of the actual distance between Farmer and Withrow.
------------
Second example
The distance between Seattle WA and Spokane WA is 225 miles
j's Distance Calculator 5.0 provides the value of 155 miles. See below:

Again, the Calculator is providing a distance that is 68 percent of the actual distance between Spokane and Seattle.
-------------
Now why is this? j's Distance Calculator is absolutely the most valuable tool to provide accurate distances between locations anywhere in the world. And I am NOT being facetious here. Its potential is enormous.
However, there is a baseline assumption that is incorrect. johannes is basing his values on the following numbers:

The Radius value of 3956.088 miles over 90 degrees Latitude yields 44 miles per degree of Latitude.
But we know that the distance between degrees of Latitude is 68 or 69 miles, correct??
We also know that there are 90 degrees of Latitude between the Equator and the North Pole. So 90 is correct.
Hence, the value of 3956.088 miles for the Radius of the circle at the Equator is incorrect, as it yields a too small a value for distance per degree of Latitude.
The actual Radius value has to be ((100 - 67) / 67 ) * 100 = 50% larger than 3956.088.
This equates to approximately 5838 miles for the Radius.
And 5838 times 2 times PI = the Circumference of a circle at the Equator = approximately 36663 statute miles.
By plugging in this adjustment to j's Distance Calculator I now arrive at 225 miles between Seattle and Spokane, and 6 miles between Withrow and Farmer WA.
Please note that there will be a close approximation of distances, North of the Equator and especially North of the Tropic of Cancer, between the j's Distance Calculator and globe model measurements.
Secondly, of note, there will be a complete match between j's Distance Calculator and globe model measuring on all Longitudinal meridians due to the fact that there is no influence of the globe on the straight lines of Longitude. For example: Point A at Longitude X to Point B on Longitude X will have the same distance value between j's Distance Calculator and the globe model measurement.
Thirdly, of note, the differences between j's DC and globe model measurements will increase the further one travels South.
I will provide the adjustment values I changed in johannes' spreadsheet in order to correct the longitudinal issue.
bdh
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
And further ramblings based upon testing with coordinates in Australia, my guesstimates remain true.
Longitudinally, any distance I measure comes up true; any distance I attempt to measure latitudinally will come up wonky. So, what do we need to do here? Grab a handfull of adventurers and head to Austrialia for 6 months. LOL
Let me clarify the difference in distance of degrees of latitude and longitude between the flat plane and the globe:
1. For degrees of longitude, the difference in degree-distance between plane and globe will be zero.... that is... no difference
2. For degrees of latitude, the difference in degree-distance between plane and globe will be:
a. very small North of the Tropic of Cancer and
b. increasingly larger as one proceed South.
This is evident by placing a flat disk on top of a ball and scribing latitude and longitude lines on each.
Longitudinally, any distance I measure comes up true; any distance I attempt to measure latitudinally will come up wonky. So, what do we need to do here? Grab a handfull of adventurers and head to Austrialia for 6 months. LOL
Let me clarify the difference in distance of degrees of latitude and longitude between the flat plane and the globe:
1. For degrees of longitude, the difference in degree-distance between plane and globe will be zero.... that is... no difference
2. For degrees of latitude, the difference in degree-distance between plane and globe will be:
a. very small North of the Tropic of Cancer and
b. increasingly larger as one proceed South.
This is evident by placing a flat disk on top of a ball and scribing latitude and longitude lines on each.
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
bdhfe,
Unfortunately I have not had the leisure to reply promptly.
(Cancer is an asshole sometimes...)
My table calculates solely on the definition of the nautical mile, without any bullet voodoo.
The path of the sun with the zenith over the equator at the equinoxes is the basis for the calculation, as I already wrote.
This results in 60 nautical miles for one degree along the equator.
This is the only value that I use in the calculation (adjusted for miles and kilometers, of course).
Everything else results from a simple circular calculation.
Of course, the distance between the longitudes changes in my calculator:
Exactly as shown in the table in Alex Gleason's book.
When entering 90° south, my DC in cell K4 or K12 gives a circumference of 43200 nautical miles as an intermediate result.
Divided by 360, that's exactly 120 nautical miles per degree.
(Thanks for confirming my DC)
Unfortunately, the equator is being raped and misused as the circumference of the ridiculous sphere.
And everyone is joining in - including Google Earth, Google Maps, etc., of course.
G-Maps uses the Merkator projection, which is nothing more than an FE map that is first wrapped around a ball, then put into a tube and the land masses are transferred to the outside and finally cut open and flattened against the zero line.
All land masses to the north are shown distorted; the further north, the more so because the smaller circumferences are stretched to the circumference of the tube.
There is enough material about this.
Unfortunately, the change in shape in the south is not shown anywhere although the topic would be very exciting...
This page makes the distortions clear; at least in the north:
https://www.thetruesize.com/
Mark the USA and drag the area towards the equator and see how the size changes...
The speedometers in our cars are also adjusted to these erroneous values; it would quickly become apparent if the distance to the neighboring town was indicated by the speedometer as 4 miles, but on traffic signs and on the web as 6 miles.
Nobody will bother to measure the distance with a folding ruler...
(I have already doubted that passenger airplanes can reach 900 kmh or 600 mph.
If you compare that with the power-to-weight ratio of kilograms per horsepower and the small frontal area of a Formula 1 racing car, it crawls over the tarmac at ridiculous speeds...)
For the degrees of longitude, a value of 60 nautical miles for one degree would also result over the surface of a spherical earth with the diameter of the equator.
Let's quickly forget this globe theory...
A degree (of longitude) is the sum of 1/90 of the radius of the equator.
The value simply results from the geometry of the circle, I have not entered it anywhere in a formula in the table.
Why were so many ships lost?
Was the available data really so wrong, or did the captains simply make the mistake of transferring the measurements to maps of the spherical model in which the distances of the longitudes converge to the south?
The Greenwich data for latitude and longitude are not wrong. But you can't transfer them to a globe if you don't want to get lost.
In addition, the entire measurement of time is based on their data.
All this is so precise that the course of the stars in the firmament can also be calculated exactly.
I would therefore leave the 12:00 UTC time and the longitude 0 as they are...
Until John Harrison built his famous ship's clocks, the course of the stars was used to set the clocks of those years to the exact time.
Astronomers knew the orbits of the stars and the time delays between them.
Harrison observed Sirius as the star disappeared behind its neighbor's chimney with the same time difference every day and then set his clocks.
The discrepancies in the coordinates in the comparison between Wikipedia and "The Australian Handbook, Almanack, Shippers' and Importers' Directory".
I could imagine that the values in the old maritime books were measured in the harbor, while Wiki may now refer to the present-day city center.
Many cities have grown a lot over time and have become metropolitan centers that can no longer be compared to the fishing villages of the 17th or 18th century.
During my research into determining longitude, I came across a PDF which, although it adores the spherical theory, describes a special method of sextant measurement for measuring the position of the sun.
This avoids the problem that the sun is at this angle for almost four minutes at its highest position.
If you measure a certain angle to the sun, e.g. 30 degrees at 11:30 a.m., then you have to observe at what time the sun has the same angle in the afternoon.
The average of the time measurements gives the exact time of the sun's highest point and thus the longitude at which you are located.

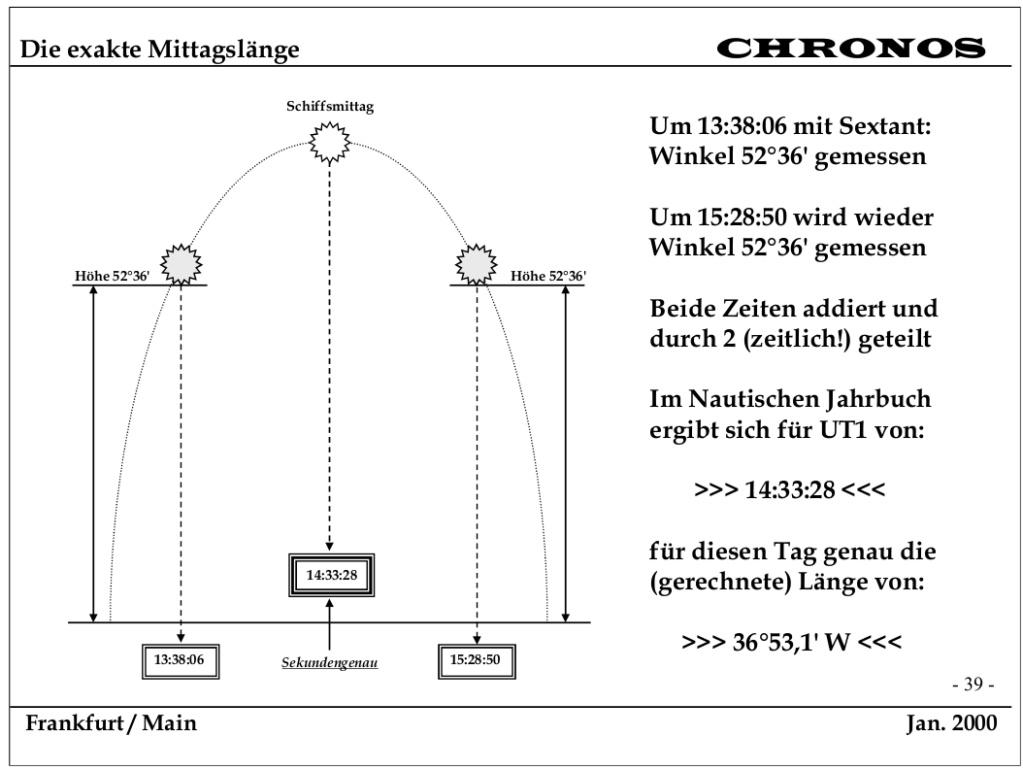
https://docplayer.org/18769750-Zeitbestimmung-auf-see.html
>>>Page 38 and 39.
It was a mystery to me how to determine the maximum position of the sun on a ship without a fixed reference point, apart from the horizon...
Without John Harrison, many more ships would probably have been lost.
James Cook had an exact replica of Harrison's masterpiece on board the Challenger when they were looking for the solution to the longitude problem.
James Cook described the clock and the method of calculation as very practicable.
After Cook's death, the Challenger was lost under a different captain...
There are some things I don't quite understand.
On the one hand, you want to be independent of Greenwich data; on the other hand, you use distance data from Google Maps, which are not necessarily known as friends of the flat earth...
The directors of this Truman show know the dimensions of the stage very well.
They enjoy how easy it is to manipulate us and sell us the most implausible stories as the truth.
The fact that you doubt the results of my calculator and fine-tune the results to Google's numbers shows how deep the globe programming goes.
If you make adjustments to get the same results as in Google Maps, you might as well throw the calculator in the garbage can.
Every official version calculates distances using a non-existent curvature of a ridiculous sphere.
I never intended to have the same numbers as everyone else as a result.
That's why I made the DC exactly as it is.
The conversion factor would be:
1 ÷ radius of the equator × quarter circle north pole - equator.
(1 ÷ 6366.707 km ×10000.80 km = 1.570796332)
In the north-south direction we extend Gleason's Australia with this factor over the globe and compress it in the east-west direction to the known shape...
Why should we do that? Because everyone is doing it?
What do we do now with the nautical mile and its siblings mile & kilometer?
Redefine them if the equator now has a much larger circumference?
Was it not just me but also Alexander Gleason who was completely wrong because we use 60 nautical miles at the equator and 120 at 90 degrees south?
If so, we must also add to the hall of fame those people who defined the nautical mile as a minute of arc or 1/60th of a degree... (Hall of fame of big errors)
(Sorry; I'm blonde on the outside but deep down there's a lot of dark humor...)
Unfortunately I have not had the leisure to reply promptly.
(Cancer is an asshole sometimes...)
My table calculates solely on the definition of the nautical mile, without any bullet voodoo.
The path of the sun with the zenith over the equator at the equinoxes is the basis for the calculation, as I already wrote.
This results in 60 nautical miles for one degree along the equator.
This is the only value that I use in the calculation (adjusted for miles and kilometers, of course).
Everything else results from a simple circular calculation.
Of course, the distance between the longitudes changes in my calculator:
Exactly as shown in the table in Alex Gleason's book.
When entering 90° south, my DC in cell K4 or K12 gives a circumference of 43200 nautical miles as an intermediate result.
Divided by 360, that's exactly 120 nautical miles per degree.
(Thanks for confirming my DC)
Unfortunately, the equator is being raped and misused as the circumference of the ridiculous sphere.
And everyone is joining in - including Google Earth, Google Maps, etc., of course.
G-Maps uses the Merkator projection, which is nothing more than an FE map that is first wrapped around a ball, then put into a tube and the land masses are transferred to the outside and finally cut open and flattened against the zero line.
All land masses to the north are shown distorted; the further north, the more so because the smaller circumferences are stretched to the circumference of the tube.
There is enough material about this.
Unfortunately, the change in shape in the south is not shown anywhere although the topic would be very exciting...
This page makes the distortions clear; at least in the north:
https://www.thetruesize.com/
Mark the USA and drag the area towards the equator and see how the size changes...
The speedometers in our cars are also adjusted to these erroneous values; it would quickly become apparent if the distance to the neighboring town was indicated by the speedometer as 4 miles, but on traffic signs and on the web as 6 miles.
Nobody will bother to measure the distance with a folding ruler...
(I have already doubted that passenger airplanes can reach 900 kmh or 600 mph.
If you compare that with the power-to-weight ratio of kilograms per horsepower and the small frontal area of a Formula 1 racing car, it crawls over the tarmac at ridiculous speeds...)
For the degrees of longitude, a value of 60 nautical miles for one degree would also result over the surface of a spherical earth with the diameter of the equator.
Let's quickly forget this globe theory...
A degree (of longitude) is the sum of 1/90 of the radius of the equator.
The value simply results from the geometry of the circle, I have not entered it anywhere in a formula in the table.
Why were so many ships lost?
Was the available data really so wrong, or did the captains simply make the mistake of transferring the measurements to maps of the spherical model in which the distances of the longitudes converge to the south?
The Greenwich data for latitude and longitude are not wrong. But you can't transfer them to a globe if you don't want to get lost.
In addition, the entire measurement of time is based on their data.
All this is so precise that the course of the stars in the firmament can also be calculated exactly.
I would therefore leave the 12:00 UTC time and the longitude 0 as they are...
Until John Harrison built his famous ship's clocks, the course of the stars was used to set the clocks of those years to the exact time.
Astronomers knew the orbits of the stars and the time delays between them.
Harrison observed Sirius as the star disappeared behind its neighbor's chimney with the same time difference every day and then set his clocks.
The discrepancies in the coordinates in the comparison between Wikipedia and "The Australian Handbook, Almanack, Shippers' and Importers' Directory".
I could imagine that the values in the old maritime books were measured in the harbor, while Wiki may now refer to the present-day city center.
Many cities have grown a lot over time and have become metropolitan centers that can no longer be compared to the fishing villages of the 17th or 18th century.
During my research into determining longitude, I came across a PDF which, although it adores the spherical theory, describes a special method of sextant measurement for measuring the position of the sun.
This avoids the problem that the sun is at this angle for almost four minutes at its highest position.
If you measure a certain angle to the sun, e.g. 30 degrees at 11:30 a.m., then you have to observe at what time the sun has the same angle in the afternoon.
The average of the time measurements gives the exact time of the sun's highest point and thus the longitude at which you are located.


https://docplayer.org/18769750-Zeitbestimmung-auf-see.html
>>>Page 38 and 39.
It was a mystery to me how to determine the maximum position of the sun on a ship without a fixed reference point, apart from the horizon...
Without John Harrison, many more ships would probably have been lost.
James Cook had an exact replica of Harrison's masterpiece on board the Challenger when they were looking for the solution to the longitude problem.
James Cook described the clock and the method of calculation as very practicable.
After Cook's death, the Challenger was lost under a different captain...
There are some things I don't quite understand.
On the one hand, you want to be independent of Greenwich data; on the other hand, you use distance data from Google Maps, which are not necessarily known as friends of the flat earth...
The directors of this Truman show know the dimensions of the stage very well.
They enjoy how easy it is to manipulate us and sell us the most implausible stories as the truth.
The fact that you doubt the results of my calculator and fine-tune the results to Google's numbers shows how deep the globe programming goes.
If you make adjustments to get the same results as in Google Maps, you might as well throw the calculator in the garbage can.
Every official version calculates distances using a non-existent curvature of a ridiculous sphere.
I never intended to have the same numbers as everyone else as a result.
That's why I made the DC exactly as it is.
The conversion factor would be:
1 ÷ radius of the equator × quarter circle north pole - equator.
(1 ÷ 6366.707 km ×10000.80 km = 1.570796332)
In the north-south direction we extend Gleason's Australia with this factor over the globe and compress it in the east-west direction to the known shape...
Why should we do that? Because everyone is doing it?
What do we do now with the nautical mile and its siblings mile & kilometer?
Redefine them if the equator now has a much larger circumference?
Was it not just me but also Alexander Gleason who was completely wrong because we use 60 nautical miles at the equator and 120 at 90 degrees south?
If so, we must also add to the hall of fame those people who defined the nautical mile as a minute of arc or 1/60th of a degree... (Hall of fame of big errors)
(Sorry; I'm blonde on the outside but deep down there's a lot of dark humor...)
Last edited by johannes.wallenfang on Wed Feb 07, 2024 5:01 pm; edited 1 time in total

johannes.wallenfang- Posts : 13
Points : 262
Reputation : 0
Join date : 2023-11-23
Age : 60
Location : Germany
 Re: Mapping the Earth
Re: Mapping the Earth
To show the bizarre shape of the Mercator projection, I took the small island off the coast of Alaska and the small island near the southern tip of Greenland.
Both are pretty much on the same latitude.
The screen ruler only served as a small help and has no meaning.
Google Maps says ~5788 km / 3596 mi.

Divided on the equator, this straight red line should fit on the equator about 6.9 times...

The shorter green line corresponds to the black equator line (in this case ~25 cm ÷ 40003.2 km× 5788 km)
Green fits; while the red line runs out of space after the third repetition...
If I calculate the distance with my calculator I get 3725 km / 2315 miles.
The angle of longitude is 122.573 degrees.
For the 60th parallel north, my table gives 7200 nautical miles as a partial result.
This agrees with Alexander Gleason's table, in which he gives 20 nautical miles.
7200 nautical miles ÷ 360 degrees × 122.573 degrees = 2451.46 nautical miles along the arc of the circle.
As a straight line distance between the coordinates, this is 2012 nautical miles.
Greenland 59.85256780446295, -43.74423554572192
Alaska 60.10067604685792, -166.31732920014505
Both are pretty much on the same latitude.
The screen ruler only served as a small help and has no meaning.
Google Maps says ~5788 km / 3596 mi.

Divided on the equator, this straight red line should fit on the equator about 6.9 times...

The shorter green line corresponds to the black equator line (in this case ~25 cm ÷ 40003.2 km× 5788 km)
Green fits; while the red line runs out of space after the third repetition...
If I calculate the distance with my calculator I get 3725 km / 2315 miles.
The angle of longitude is 122.573 degrees.
For the 60th parallel north, my table gives 7200 nautical miles as a partial result.
This agrees with Alexander Gleason's table, in which he gives 20 nautical miles.
7200 nautical miles ÷ 360 degrees × 122.573 degrees = 2451.46 nautical miles along the arc of the circle.
As a straight line distance between the coordinates, this is 2012 nautical miles.
Greenland 59.85256780446295, -43.74423554572192
Alaska 60.10067604685792, -166.31732920014505

johannes.wallenfang- Posts : 13
Points : 262
Reputation : 0
Join date : 2023-11-23
Age : 60
Location : Germany
 Re: Mapping the Earth
Re: Mapping the Earth
Hi johannes,
Great post!! I have not read through the whole article as yet, but want to say a couple of things.
First, I am sorry to hear of your mention of cancer. Best wishes for a good outcome in handling it.
Second, your mention of nautical miles in your post has pinged something in my mind that should be addressed.
From a high level (no pun intended) the issue to be addressed is: What is the true conversion between nautical and statute miles??
It is 60 nautical miles, as you and Gleason say, between each degree of longitude at the equator.
By globe definition, this equates to 69.04 statute miles per degree.
But is this true? Is it 69.04 statute miles per 60 nautical miles? Remember the nautical mile is based on a globe calculations..... used in maritime and aviation distances.
Let's bring Latitude into this calculation. On the flat earth, is not the distance in degrees of latitude about 69 statute miles per degree? If so, does not the circumference at the equator now expand to the 36K+ statute miles I calculated earlier?
So, there is a mismatch here. Longitude says 24K+ statute miles, Latitude says 36K+ statute miles.
I agree that there is a STANDARDS manipulation going on here in order to deceive the world, and I believe you have hit the nail on the proverbial head when you mentioned this.
I believe the manipulation has to do with the nautical mile -- statute mile conversion.
There are too few statute miles arrived at per nautical mile. They say that 1 nautical mile = 1.15078 statute miles
Given: 21600 nautical miles is the circumference of the Earth at the equator
Given: There are approximately 69 statute miles per degree of Latitude.
Ergo, the distance between the North Pole and the Equator is 6210 statute miles, thus giving the value of approximately 40K statute miles at the Equator.
Latitude says 40K statute miles for circumference, Longitude says 21600 nautical miles for circumference
This equates to 1.805 statute miles per 1 nautical mile and not 1.15 as the globe creatures estimate.
What does Longitude say about Equatorial circumference statute mile wise? Nothing but the globe nautical mile conversion value in our globe based textbooks.... 1.15
The conversion value of 1.805 would certainly go a long way to explain the mariners' issues when traveling east towards Africa and being told they have crossed the Cape of Good Hope but in reality are still WEST of Africa.
Again, great post johannes!
Great post!! I have not read through the whole article as yet, but want to say a couple of things.
First, I am sorry to hear of your mention of cancer. Best wishes for a good outcome in handling it.
Second, your mention of nautical miles in your post has pinged something in my mind that should be addressed.
From a high level (no pun intended) the issue to be addressed is: What is the true conversion between nautical and statute miles??
It is 60 nautical miles, as you and Gleason say, between each degree of longitude at the equator.
By globe definition, this equates to 69.04 statute miles per degree.
But is this true? Is it 69.04 statute miles per 60 nautical miles? Remember the nautical mile is based on a globe calculations..... used in maritime and aviation distances.
Let's bring Latitude into this calculation. On the flat earth, is not the distance in degrees of latitude about 69 statute miles per degree? If so, does not the circumference at the equator now expand to the 36K+ statute miles I calculated earlier?
So, there is a mismatch here. Longitude says 24K+ statute miles, Latitude says 36K+ statute miles.
I agree that there is a STANDARDS manipulation going on here in order to deceive the world, and I believe you have hit the nail on the proverbial head when you mentioned this.
I believe the manipulation has to do with the nautical mile -- statute mile conversion.
There are too few statute miles arrived at per nautical mile. They say that 1 nautical mile = 1.15078 statute miles
Given: 21600 nautical miles is the circumference of the Earth at the equator
Given: There are approximately 69 statute miles per degree of Latitude.
Ergo, the distance between the North Pole and the Equator is 6210 statute miles, thus giving the value of approximately 40K statute miles at the Equator.
Latitude says 40K statute miles for circumference, Longitude says 21600 nautical miles for circumference
This equates to 1.805 statute miles per 1 nautical mile and not 1.15 as the globe creatures estimate.
What does Longitude say about Equatorial circumference statute mile wise? Nothing but the globe nautical mile conversion value in our globe based textbooks.... 1.15
The conversion value of 1.805 would certainly go a long way to explain the mariners' issues when traveling east towards Africa and being told they have crossed the Cape of Good Hope but in reality are still WEST of Africa.
Again, great post johannes!
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
 Re: Mapping the Earth
Re: Mapping the Earth
Hello bdhfe,
You can trust the usual conversions (miles to nautical miles to kilometers).
However, 60 nautical miles or 69 miles have absolutely nothing to do with the distance between latitudes along a longitude.
This is only the case with the believers in spheres because we have always been told so.

Quote from you:
Given: 21600 nautical miles is the circumference of the earth at the equator
Once again:
The equator is the circle of the sun at the equinoxes.
It is only raped to the diameter of a sphere.
Alex Gleason wrote in his book that the sun travels at exactly 900 nautical miles per hour across this latitude on these days.
He also wrote that the sun slows down to the north and speeds up to the south.
Quote from you:
Given: There are approximately 69 statute miles per degree of Latitude.
Ergo, the distance between the North Pole and the Equator is 6210 statute miles, thus giving the value of approximately 40K statute miles at the Equator.
FALSE
According to the abstruse theory of the globe disciples, 1 degree is 60 nautical miles or 69 miles.
Swapping the designations leads to incorrect values.
If the equator of the globe were tilted 90 degrees so that it was over the North Pole, then a quarter of this circle would have curved ~6210 miles or ~5400 nautical miles from the globe's North Pole to the globe's equator.
Quote from you:
The conversion value of 1.805 would certainly go a long way to explain the mariners' issues when traveling east towards Africa and being told they have crossed the Cape of Good Hope but in reality are still WEST of Africa.
All I say to that is that the captains would have been better off looking at Gleason's chart and doing their navigation on the flat earth map because the latitudes to the south have larger radii / circumferences.
Quote from you:
Let's bring Latitude into this calculation. On the flat earth, is not the distance in degrees of latitude about 69 statute miles per degree? If so, does not the circumference at the equator now expand to the 36K+ statute miles I calculated earlier?
So there is an inconsistency here. The longitude says 24K+ statute miles, the latitude says 36K+ statute miles.
No!
Where do these 36,000 miles actually come from?
Are you possibly calculating a egg shaped Mars? (Sorry)
--------------------------------------
Seemeile (Deutsch) aus Wikipedia:
Die Seemeile ist eine in der Schiff- und Luftfahrt gebräuchliche Längeneinheit. Die Seemeile wurde 1929 auf der "Internationalen Hydrographischen Konferenz" in Monaco auf 1.852 m festgelegt.
Vor dieser Konferenz war die Seemeile als die Strecke einer Bogenminute am Äquator definiert. Ein Vollkreis enthält 360 Grad, mit 60 Minuten je Grad, also insgesamt 21600 Minuten. Damit war die Seemeile der 21600ste Teil des Erdumfangs am Äquator.
--------------------------------------
Nautical mile, translated:
The nautical mile is a unit of length commonly used in shipping and aviation. The nautical mile was defined as 1,852 m at the "International Hydrographic Conference" in Monaco in 1929.
Before this conference, the nautical mile was defined as the distance of one minute of arc at the equator.
A full circle contains 360 degrees, with 60 minutes per degree, i.e. a total of 21600 minutes. The nautical mile was therefore the 21600th part of the Earth's circumference at the equator.
--------------------------------------
Of course, they go on to spread the globe nonsense and write that this measurement also applies to longitude.
As a globe dealer you have to do it that way...
You can trust the usual conversions (miles to nautical miles to kilometers).
However, 60 nautical miles or 69 miles have absolutely nothing to do with the distance between latitudes along a longitude.
This is only the case with the believers in spheres because we have always been told so.

Quote from you:
Given: 21600 nautical miles is the circumference of the earth at the equator
Once again:
The equator is the circle of the sun at the equinoxes.
It is only raped to the diameter of a sphere.
Alex Gleason wrote in his book that the sun travels at exactly 900 nautical miles per hour across this latitude on these days.
He also wrote that the sun slows down to the north and speeds up to the south.
Quote from you:
Given: There are approximately 69 statute miles per degree of Latitude.
Ergo, the distance between the North Pole and the Equator is 6210 statute miles, thus giving the value of approximately 40K statute miles at the Equator.
FALSE
According to the abstruse theory of the globe disciples, 1 degree is 60 nautical miles or 69 miles.
Swapping the designations leads to incorrect values.
If the equator of the globe were tilted 90 degrees so that it was over the North Pole, then a quarter of this circle would have curved ~6210 miles or ~5400 nautical miles from the globe's North Pole to the globe's equator.
Quote from you:
The conversion value of 1.805 would certainly go a long way to explain the mariners' issues when traveling east towards Africa and being told they have crossed the Cape of Good Hope but in reality are still WEST of Africa.
All I say to that is that the captains would have been better off looking at Gleason's chart and doing their navigation on the flat earth map because the latitudes to the south have larger radii / circumferences.
Quote from you:
Let's bring Latitude into this calculation. On the flat earth, is not the distance in degrees of latitude about 69 statute miles per degree? If so, does not the circumference at the equator now expand to the 36K+ statute miles I calculated earlier?
So there is an inconsistency here. The longitude says 24K+ statute miles, the latitude says 36K+ statute miles.
No!
Where do these 36,000 miles actually come from?
Are you possibly calculating a egg shaped Mars? (Sorry)
--------------------------------------
Seemeile (Deutsch) aus Wikipedia:
Die Seemeile ist eine in der Schiff- und Luftfahrt gebräuchliche Längeneinheit. Die Seemeile wurde 1929 auf der "Internationalen Hydrographischen Konferenz" in Monaco auf 1.852 m festgelegt.
Vor dieser Konferenz war die Seemeile als die Strecke einer Bogenminute am Äquator definiert. Ein Vollkreis enthält 360 Grad, mit 60 Minuten je Grad, also insgesamt 21600 Minuten. Damit war die Seemeile der 21600ste Teil des Erdumfangs am Äquator.
--------------------------------------
Nautical mile, translated:
The nautical mile is a unit of length commonly used in shipping and aviation. The nautical mile was defined as 1,852 m at the "International Hydrographic Conference" in Monaco in 1929.
Before this conference, the nautical mile was defined as the distance of one minute of arc at the equator.
A full circle contains 360 degrees, with 60 minutes per degree, i.e. a total of 21600 minutes. The nautical mile was therefore the 21600th part of the Earth's circumference at the equator.
--------------------------------------
Of course, they go on to spread the globe nonsense and write that this measurement also applies to longitude.
As a globe dealer you have to do it that way...

johannes.wallenfang- Posts : 13
Points : 262
Reputation : 0
Join date : 2023-11-23
Age : 60
Location : Germany
 Re: Mapping the Earth
Re: Mapping the Earth
johannes.wallenfang wrote:Hello bdhfe,
You can trust the usual conversions (miles to nautical miles to kilometers).
However, 60 nautical miles or 69 miles have absolutely nothing to do with the distance between latitudes along a longitude.
This is only the case with the believers in spheres because we have always been told so.
johannes,
My mistake! The illustration you provided above is BS and not what you are averring..... It certainly put me off into the weeds as a result.
johannes.wallenfang wrote:
Quote from you:
Given: 21600 nautical miles is the circumference of the earth at the equator
Once again:
The equator is the circle of the sun at the equinoxes.
It is only raped to the diameter of a sphere.
I completely agree.
johannes.wallenfang wrote:
Alex Gleason wrote in his book that the sun travels at exactly 900 nautical miles per hour across this latitude on these days.
He also wrote that the sun slows down to the north and speeds up to the south.
Yes.
johannes.wallenfang wrote:
Quote from you:
Given: There are approximately 69 statute miles per degree of Latitude.
Ergo, the distance between the North Pole and the Equator is 6210 statute miles, thus giving the value of approximately 40K statute miles at the Equator.
FALSE
According to the abstruse theory of the globe disciples, 1 degree is 60 nautical miles or 69 miles.
Swapping the designations leads to incorrect values.
If the equator of the globe were tilted 90 degrees so that it was over the North Pole, then a quarter of this circle would have curved ~6210 miles or ~5400 nautical miles from the globe's North Pole to the globe's equator.
Based on what your graphic above, and of what I assumed was not BS, I see what you are saying. Agreed.
johannes.wallenfang wrote:
Quote from you:
Let's bring Latitude into this calculation. On the flat earth, is not the distance in degrees of latitude about 69 statute miles per degree? If so, does not the circumference at the equator now expand to the 36K+ statute miles I calculated earlier?
So there is an inconsistency here. The longitude says 24K+ statute miles, the latitude says 36K+ statute miles.
No!
Where do these 36,000 miles actually come from?
Are you possibly calculating a egg shaped Mars? (Sorry)
LOL, Possibly!
johannes.wallenfang wrote:
Nautical mile, translated:
The nautical mile is a unit of length commonly used in shipping and aviation. The nautical mile was defined as 1,852 m at the "International Hydrographic Conference" in Monaco in 1929.
Before this conference, the nautical mile was defined as the distance of one minute of arc at the equator.
A full circle contains 360 degrees, with 60 minutes per degree, i.e. a total of 21600 minutes. The nautical mile was therefore the 21600th part of the Earth's circumference at the equator.
--------------------------------------
Of course, they go on to spread the globe nonsense and write that this measurement also applies to longitude.
As a globe dealer you have to do it that way...
Thank you for this:
Before this conference, the nautical mile was defined as the distance of one minute of arc at the equator.
A full circle contains 360 degrees, with 60 minutes per degree, i.e. a total of 21600 minutes. The nautical mile was therefore the 21600th part of the Earth's circumference at the equator.
Question then: What is the circumference of the circle around the equator?
bdhfe- Posts : 77
Points : 1896
Reputation : 6
Join date : 2019-08-12
Page 4 of 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 Similar topics
Similar topics» Experiments We All Can Do
» The Earth Plane (Flat Earth Children's Book)
» Flat Earth Audiobooks and PDFs
» Eric Dubay and IFERS Banned From the Internet
» Promoting Flat Earth
» The Earth Plane (Flat Earth Children's Book)
» Flat Earth Audiobooks and PDFs
» Eric Dubay and IFERS Banned From the Internet
» Promoting Flat Earth
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: Reference Materials, eBooks, Articles, Videos, Maps
Page 4 of 5
Permissions in this forum:
You cannot reply to topics in this forum|
|
|

