Einstein's math and airline gyroscopes prove flat earth.
3 posters
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: Heliocentricity, Geocentricity, Cosmology and Cosmogeny
Page 1 of 1
 Einstein's math and airline gyroscopes prove flat earth.
Einstein's math and airline gyroscopes prove flat earth.
The math apparatus developed by Einstein and his controllers to fool the masses, was impressive and even if the Einstein's Field Equations per se are ridiculous, the math apparatus includes a mathematical method to learn the curvature of a surface. The method (explained in the video segment below), is based on parallel-translation of a vector around a curve of the surface examined. I recommend watching from start if you you want a crash course in tensor math.
https://youtu.be/foRPKAKZWx8?t=4353
As you know after watching 5 minutes (to 1:17:30), you will know that if you parallel-transport a vector around substantial loop on a surface and end up with the vector pointing in a different angle from the direction you started with, then the surface under that travel-loop, is curved, and the drift in angle of the vector is a measure of that curvature. Of course as most are able to figure out, flat earth is ... flat i.e. it has no curvature, and consequently, no such drift of angle will happen.
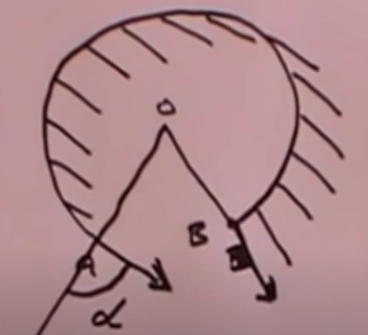
SO, if we are able to take a trip around (say) a US State or half of Europe, and are able to to surely parallel-transpose our vector along the way, then, arriving back at our starting-point, we will know the answer without doubt. If the Earth is curved, then we will have a substantial deviation in angle from our initial vector and if the earth is flat, we might have a miniscule drift due to all kinds of things but curvature.

So how can we assure that a vector is parallel-transposed throughout a potentially very long trip, i.e. always having it pointing in the same direction, no matter where we go?
Answer : With a Gyroscope. - Calibrate a fully analog gyroscope at the starting point and travel in a convex path back to the starting point and check for substantial drift after the finish. Be sure to avoid gyro's that have the add-on 'correcting' mechanics or electronics.
This means that one whole new way to test the validity ball earth, is to make a research study into gyro accuracy in cooperation with an airline.
But hold on ... one strategy for that evaluation is essentially already being executed for us more than 100.000 times per day, by the airlines.
IF the earth really was a ball 25000 miles in circumference, this so called "holonomy or geometric phase" (H) or "angle drift", (Δθ), would be a substantial amount and constant for the entire Earth, regardless of how the (assumed convex) loop of travel looks like.
So, how large would the holonomy of the alledged ball Earth be?
The angular holonomy in tensor terms, H = Δθ can generally be expressed as
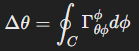
Where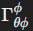 is the he Christoffel symbol of the second kind for the polar coordinates (θ,ϕ) of the surface, and the integral is taken over the closed loop C parameterized by the azimuthal angle ϕ.
is the he Christoffel symbol of the second kind for the polar coordinates (θ,ϕ) of the surface, and the integral is taken over the closed loop C parameterized by the azimuthal angle ϕ.
Applied to a spherical earth, the above tensor-integration becomes a line integral of
H = Δθ =
Where and r(t) is a parameterization of our traveling loop. We recognize that since an integral is summation, we could have both positive and negative curvatures along an unknown surface. So in order to know the nature of an unknown surface, we need to evaluate many loops over it. However, assuming a ball Earth with radius R=6371 kilometers =3959 miles, the integral can be computed numerically. And, if we do this, we find that the angular holonomy (H or Δθ) for ball Earth theoretically should be about 1.486 radians or 85.14 degrees. Due to the uniform nature of the sphere, the holonomy of ball Earth is theoretically constant, as here verified by calculation of the line integral above, using official globe-earth latitudes and longitudes for 10 different traveling loops between major cities:
Loop 1: New York - Los Angeles - Mexico City - New York --> H = 1.486 radians
Loop 2: London - Paris - Berlin - London --> H = 1.486 radians
Loop 3: Tokyo - Sydney - Auckland - Tokyo --> H = 1.486 radians
Loop 4: Dubai - Mumbai - Singapore - Dubai --> H = 1.486 radians
Loop 5: Moscow - Beijing - Seoul - Moscow --> H = 1.486 radians
Loop 6: Cape Town - Nairobi - Cairo - Cape Town --> H = 1.486 radians
Loop 7: Buenos Aires - Santiago - Lima - Buenos Aires --> H = 1.486 radians
Loop 8: Toronto - Vancouver - Montreal - Toronto --> H = 1.486 radians
Loop 9: Rio de Janeiro - Bogota - Caracas - Rio de Janeiro --> H = 1.486 radians
Loop 10: Istanbul - Athens - Rome - Istanbul --> H = 1.486 radians
((As a paranthesis, we can note that the GPS coordinates of these cities are taken from official sources.
This means that GPS is officially debunking the Earth as being an oblate spheroid.
The extremely small and consistent variance in the results of these calculations, also indicate that GPS is very likley using a model and not real measurements.))
To make it clear: On ball Earth, regardless if an airliner travels halfway around the world and back or just a regional round-trip, its gyro would in principle drift more than 85 degrees from the direction it was calibrated towards before the start. That's just not some crazy conspiracy theory, but the real, mathematical/physical consequence of curvature of ball Earth. And using GPS and "sensor fusion" to try solve the problem, would defeat the whole purpose of the gyro in the first place and still would not be enough to fully know and handle the problem.
Now, High-quality flight navigation systems used in airliners, have an accuracy better than (drift in angle less than) 0.1 degrees per hour, including ALL possible sources of errors prompting recalibrations of the gyroscope, combined. Consequently, a huge repeated (partly random) drift more than 850 times greater that all other drift-effects combined, would make a gyro completely useless, and absolutely out of the question from a flight safety point-of-view. Even on an oblate spheroid Earth, the weakest curvature would still render angular drift that is 100s of times greater than the 0.1 degrees per hour margin or error.
Practically, we just need to move in a loop wide enough for the gyro to actually be able to detect the differences in angle. - Looping around in our own living-room with a hand-held gyro, will likely not be enough. On the ball Earth, one degree latitude would be like 60 miles in the original (pre 1929) definition, or 96.6 km or about 70 miles / 112 km in the current definition. - It would be an interesting experiment to see at what size of traveling loop, the effect starts to practically take effect. - Get a gyro for your next road-trip!

Essentially, the only viable solution would be to recalibrate the gyro's on all airliners after every single trip and even mid flight.
- Is that happening?
Short answer : No. Gyroscopes and other sensitive navigation sensors only undergo calibration procedures on a monthly basis for all kinds of reasons, including:
No mention at all of recalibration being done due to drift from the Earth being curved ...
So what about it? Are recalibrations done at least partly to reset the huge angular drift on the globe?
Again, No.
True. A gyro has no awareness of the nature of the surface it's moving over. -That's why it works. But ofc then, the navigation and flight planning systems are not able to know how the gyro is drifting and neither able to (nor purposed to) be compensating for the gyro going bonkers vs. the a ball Earth curvature every second flight. It's clear that no maintenance schedule in the world would be able to keep up with the insane amount of angular flips that would happen on a ball Earth.
And yet, here we are, having used gyros for decades, throughout most of modern flight, doing maintenances monthly, once per 200-400 trips, and according to experts, even bi-yearly(!) 100.000 regional and worldwide flights daily, by commercial airliners alone. In total, we are talking about a million of gyro-supported air-travels of all kinds every single day! And NONE of them are reporting a +85 degrees havoc in their gyros.
Conclusion :
All modern flight, in combination with curvature math, PROVE that angular holonomy is a non-existent phenomena i.e. that Earth is flat.
The consistent absence of actual measured angluar drift (holonomy) , show that
https://youtu.be/foRPKAKZWx8?t=4353
As you know after watching 5 minutes (to 1:17:30), you will know that if you parallel-transport a vector around substantial loop on a surface and end up with the vector pointing in a different angle from the direction you started with, then the surface under that travel-loop, is curved, and the drift in angle of the vector is a measure of that curvature. Of course as most are able to figure out, flat earth is ... flat i.e. it has no curvature, and consequently, no such drift of angle will happen.

SO, if we are able to take a trip around (say) a US State or half of Europe, and are able to to surely parallel-transpose our vector along the way, then, arriving back at our starting-point, we will know the answer without doubt. If the Earth is curved, then we will have a substantial deviation in angle from our initial vector and if the earth is flat, we might have a miniscule drift due to all kinds of things but curvature.

So how can we assure that a vector is parallel-transposed throughout a potentially very long trip, i.e. always having it pointing in the same direction, no matter where we go?
Answer : With a Gyroscope. - Calibrate a fully analog gyroscope at the starting point and travel in a convex path back to the starting point and check for substantial drift after the finish. Be sure to avoid gyro's that have the add-on 'correcting' mechanics or electronics.
This means that one whole new way to test the validity ball earth, is to make a research study into gyro accuracy in cooperation with an airline.
But hold on ... one strategy for that evaluation is essentially already being executed for us more than 100.000 times per day, by the airlines.
IF the earth really was a ball 25000 miles in circumference, this so called "holonomy or geometric phase" (H) or "angle drift", (Δθ), would be a substantial amount and constant for the entire Earth, regardless of how the (assumed convex) loop of travel looks like.
So, how large would the holonomy of the alledged ball Earth be?
The angular holonomy in tensor terms, H = Δθ can generally be expressed as
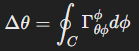
Where
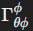 is the he Christoffel symbol of the second kind for the polar coordinates (θ,ϕ) of the surface, and the integral is taken over the closed loop C parameterized by the azimuthal angle ϕ.
is the he Christoffel symbol of the second kind for the polar coordinates (θ,ϕ) of the surface, and the integral is taken over the closed loop C parameterized by the azimuthal angle ϕ.Applied to a spherical earth, the above tensor-integration becomes a line integral of
H = Δθ =

Where and r(t) is a parameterization of our traveling loop. We recognize that since an integral is summation, we could have both positive and negative curvatures along an unknown surface. So in order to know the nature of an unknown surface, we need to evaluate many loops over it. However, assuming a ball Earth with radius R=6371 kilometers =3959 miles, the integral can be computed numerically. And, if we do this, we find that the angular holonomy (H or Δθ) for ball Earth theoretically should be about 1.486 radians or 85.14 degrees. Due to the uniform nature of the sphere, the holonomy of ball Earth is theoretically constant, as here verified by calculation of the line integral above, using official globe-earth latitudes and longitudes for 10 different traveling loops between major cities:
Loop 1: New York - Los Angeles - Mexico City - New York --> H = 1.486 radians
Loop 2: London - Paris - Berlin - London --> H = 1.486 radians
Loop 3: Tokyo - Sydney - Auckland - Tokyo --> H = 1.486 radians
Loop 4: Dubai - Mumbai - Singapore - Dubai --> H = 1.486 radians
Loop 5: Moscow - Beijing - Seoul - Moscow --> H = 1.486 radians
Loop 6: Cape Town - Nairobi - Cairo - Cape Town --> H = 1.486 radians
Loop 7: Buenos Aires - Santiago - Lima - Buenos Aires --> H = 1.486 radians
Loop 8: Toronto - Vancouver - Montreal - Toronto --> H = 1.486 radians
Loop 9: Rio de Janeiro - Bogota - Caracas - Rio de Janeiro --> H = 1.486 radians
Loop 10: Istanbul - Athens - Rome - Istanbul --> H = 1.486 radians
((As a paranthesis, we can note that the GPS coordinates of these cities are taken from official sources.
This means that GPS is officially debunking the Earth as being an oblate spheroid.
The extremely small and consistent variance in the results of these calculations, also indicate that GPS is very likley using a model and not real measurements.))
To make it clear: On ball Earth, regardless if an airliner travels halfway around the world and back or just a regional round-trip, its gyro would in principle drift more than 85 degrees from the direction it was calibrated towards before the start. That's just not some crazy conspiracy theory, but the real, mathematical/physical consequence of curvature of ball Earth. And using GPS and "sensor fusion" to try solve the problem, would defeat the whole purpose of the gyro in the first place and still would not be enough to fully know and handle the problem.
Now, High-quality flight navigation systems used in airliners, have an accuracy better than (drift in angle less than) 0.1 degrees per hour, including ALL possible sources of errors prompting recalibrations of the gyroscope, combined. Consequently, a huge repeated (partly random) drift more than 850 times greater that all other drift-effects combined, would make a gyro completely useless, and absolutely out of the question from a flight safety point-of-view. Even on an oblate spheroid Earth, the weakest curvature would still render angular drift that is 100s of times greater than the 0.1 degrees per hour margin or error.
Practically, we just need to move in a loop wide enough for the gyro to actually be able to detect the differences in angle. - Looping around in our own living-room with a hand-held gyro, will likely not be enough. On the ball Earth, one degree latitude would be like 60 miles in the original (pre 1929) definition, or 96.6 km or about 70 miles / 112 km in the current definition. - It would be an interesting experiment to see at what size of traveling loop, the effect starts to practically take effect. - Get a gyro for your next road-trip!

Essentially, the only viable solution would be to recalibrate the gyro's on all airliners after every single trip and even mid flight.
- Is that happening?
Short answer : No. Gyroscopes and other sensitive navigation sensors only undergo calibration procedures on a monthly basis for all kinds of reasons, including:
- Wear and Tear: Continuous operation and mechanical stress on gyroscopic components can lead to gradual wear and degradation. Friction, vibration, and mechanical shocks experienced during flight can affect the precision of the gyroscopes.
- Temperature Variations: Changes in temperature can impact the performance of gyroscopic systems. Gyros are sensitive to temperature fluctuations, and variations in ambient temperature can cause expansion or contraction of components, affecting their alignment and accuracy.
- Environmental Conditions: Factors such as humidity, atmospheric pressure, and exposure to contaminants can also affect gyro performance. Moisture, dust, and other environmental factors can infiltrate gyroscopic components, causing corrosion, electrical interference, or mechanical issues.
- Electrical Noise: Electromagnetic interference (EMI) and radio frequency interference (RFI) from onboard electronics, avionics systems, or external sources can disrupt the operation of gyroscopes, leading to inaccuracies in measurement and drift in performance.
- Mechanical Misalignments: Misalignments or imbalances in gyroscopic components can occur due to improper installation, maintenance, or handling. Mechanical distortions or misalignments can lead to irregularities in gyro performance and contribute to drift over time.
- Aging and Component Degradation: Over time, gyroscopic components may experience aging-related degradation, such as material fatigue, corrosion, or component failure. Aging components may exhibit reduced performance or increased susceptibility to drift, necessitating periodic calibration and maintenance.
- Calibration Errors: Inaccuracies in initial calibration or subsequent adjustments can also contribute to gyro drift. Improper calibration procedures, calibration drift, or inaccuracies in calibration equipment can introduce errors into the gyroscopic measurements.
No mention at all of recalibration being done due to drift from the Earth being curved ...
So what about it? Are recalibrations done at least partly to reset the huge angular drift on the globe?
Again, No.
"... Recalibration of gyroscopes in aircraft is not typically performed due to the curvature of the Earth. These gyroscopes operate based on the principles of angular momentum and are unaffected by the shape of the Earth. ... The curvature of the Earth is accounted for in the navigation and flight planning systems ... [which] ... incorporate accurate geographic and geodetic data, including the Earth's curvature, to calculate flight paths, positions, and headings." |

And yet, here we are, having used gyros for decades, throughout most of modern flight, doing maintenances monthly, once per 200-400 trips, and according to experts, even bi-yearly(!) 100.000 regional and worldwide flights daily, by commercial airliners alone. In total, we are talking about a million of gyro-supported air-travels of all kinds every single day! And NONE of them are reporting a +85 degrees havoc in their gyros.
Conclusion :
All modern flight, in combination with curvature math, PROVE that angular holonomy is a non-existent phenomena i.e. that Earth is flat.
The consistent absence of actual measured angluar drift (holonomy) , show that
- The topology of Earth CANNOT BE a spheroid (oblate or not). The necessary consistent amount of drift of > 85 degrees for a ball Earth with 3959 miles radius, has simply never been detected.
- The topology of Earth HAS TO BE flat. There is only one topology that consistently exhibits zero angular holonomy : A plat plane. If Earth wasn't flat, then there would be some area (large or small) where the gyros would exhibit a holonomy substantially (>850 times) above the normal operational drift of 0.1 degrees per hour. Again, NO such area or flight path (locally, regionally or world-wide) has been reported during the first 100 years of 100.000 to 1 million gyro-guided daily flights consistently flying in all kinds of paths over the Earth. Let alone any consistent deviation independent of flight path.
Last edited by PacMan on Sun Nov 17, 2024 4:15 pm; edited 87 times in total
PacMan- Posts : 21
Points : 1284
Reputation : 1
Join date : 2021-07-20
!!!, Ruth441 and TyrannicalSawdustRex like this post
 Re: Einstein's math and airline gyroscopes prove flat earth.
Re: Einstein's math and airline gyroscopes prove flat earth.
Wasted about 40 mins watching the vid about Einstein and his relatives . Waste of time . Pure imaginary bs for theoretic (i.e. imaginary ) physics and spacetime nonsense.
The use of Christoffel symbols out lined here
https://profoundphysics.com/christoffel-symbols-a-complete-guide-with-examples/
Christoffel symbols ,as stated in the link , represent fictional forces - couldn't get any sillier imo. Profound physics my arse. Everything based on assumption - the main unprovable assumption being the globe. They are obviously unable to show it to us hence the mathy gobshite , excuse my French.
Didn't get as far as the Holonomy phenomony - glad to see you reached the obvious conclusion for that one
There are some threads on here ,I think , about the gyroscopes demonstrating the stationary plane.
The use of Christoffel symbols out lined here
https://profoundphysics.com/christoffel-symbols-a-complete-guide-with-examples/
Christoffel symbols ,as stated in the link , represent fictional forces - couldn't get any sillier imo. Profound physics my arse. Everything based on assumption - the main unprovable assumption being the globe. They are obviously unable to show it to us hence the mathy gobshite , excuse my French.
Didn't get as far as the Holonomy phenomony - glad to see you reached the obvious conclusion for that one
There are some threads on here ,I think , about the gyroscopes demonstrating the stationary plane.
TyrannicalSawdustRex- Posts : 91
Points : 771
Reputation : 1
Join date : 2023-01-14
Location : BritishIsles
!!!, CoffeeBean and PacMan like this post
 Re: Einstein's math and airline gyroscopes prove flat earth.
Re: Einstein's math and airline gyroscopes prove flat earth.
Very informative
Ruth441- Posts : 17
Points : 1039
Reputation : 0
Join date : 2022-02-09
 Re: Einstein's math and airline gyroscopes prove flat earth.
Re: Einstein's math and airline gyroscopes prove flat earth.
TyrannicalSawdustRex wrote:... They are obviously unable to show it to us hence the mathy gobshite , excuse my French.
Agree.
Just love the irony of the 'gobshite' ending up destroying their religion.
As examplified in this case, the mathematical apparatus these occultist developed, is impressive and correct in itself.
It might be useful to us sometime going forward, as we make real science, even if they developed it to deceive the world.
PacMan- Posts : 21
Points : 1284
Reputation : 1
Join date : 2021-07-20
TyrannicalSawdustRex likes this post
 Similar topics
Similar topics» $1,500,000 Challenge to Prove The Earth is Flat!
» The Sun, Moon, and Stars Prove the Flat Earth
» Light and Shadows Prove the Flat Earth
» The Natural Physics of Water Prove Earth Flat
» Gravity Does Not Exist!
» The Sun, Moon, and Stars Prove the Flat Earth
» Light and Shadows Prove the Flat Earth
» The Natural Physics of Water Prove Earth Flat
» Gravity Does Not Exist!
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: Heliocentricity, Geocentricity, Cosmology and Cosmogeny
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum