Direct Vision, Rationality, Realism and Common Sense.
+14
Realearth
liminoid
Admin
Real World
FL@T-E@RTH
Ziggy Kelleher
RelearningLogic
lizardking
Schpankme
dnawebma
thesilentone
Occamania
csp
vortexpuppy
18 posters
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: The International Flat Earth Research Society
Page 1 of 5
Page 1 of 5 • 1, 2, 3, 4, 5 
 Direct Vision, Rationality, Realism and Common Sense.
Direct Vision, Rationality, Realism and Common Sense.
Direct Vision, Rationality, Realism and Common Sense.
Introduction
I’ve started this as a new topic, because it covers a range of things indirectly related to the Flat Earth and difficult to slot into an existing category. In addition, there is background material of a general nature to convey on vision, geometry, philosophy, arts, etc. to (hopefully) make the connections and conclusions clear.
As I approach my 2nd anniversary on the flat earth, I remain intrigued and eager to discover how the deception is/was perpetuated and how it fooled (and continues to fool), so many people. It is clear that the deception is on multiple levels within mathematics, physics, astronomy, geology, archaeology, cosmology, arts, philosophy, language, etc., but there do appear to be key components on which the deception depends.
I think a cornerstone (or capstone ;-) of the deception is concealed in the nature of vision, the laws of optical instruments and certain mathematical theories of geometrical spaces.
Our eyes convey the most important sense data that we receive and are consequently instrumental in shaping our perceptions and beliefs. Hence the obsession of the ruling criminals with the “all-seeing eye” and one-eyed symbolism. I think they are hiding the truth in plain sight.
Before we go into detail, let me try and sum up my conclusion in one paragraph:
We have been deceived into believing, that we possess (Euclidean) vision, incapable of sensing an infinite, non-Euclidean universe. The opposite is true. Our vision is non-Euclidean and we are experiencing a finite Euclidean reality.
I am cautiously aware that the language and terminology used, might not mean the same to everybody (e.g. non-Euclidean) and will try to be as precise as possible.
Many thanks to IFERS and the research and studies of many people, too numerous to mention both dead and alive. I have freely consolidated their ideas with my own research to form the above conclusion.
Knowing that Space, et al. is fake, assisted me greatly when reviewing older manuscripts of smart people and interpreting their theories and insights in a different light. I’m sure some if some of them had known what we know now, they might also have interpreted their findings differently. In that sense, we digital natives have an advantage, since we can exclude interpretations we know to be false, leaving more of the truth exposed.
References can be found by searching the internet and thinking for yourself ;-)
All errors are of my own making.
Some essential and important reference materials.
1. Thomas Reid a Scots Minister, Regent and Natural Philosopher
https://en.wikipedia.org/wiki/Thomas_Reid
https://en.wikipedia.org/wiki/Scottish_Common_Sense_Realism
As a regent, he was an accomplished polymath, but grounded in common sense. In my opinion he wiped the floor with his contemporaries such as Bishop Berkeley, Hume, Locke, Kant and many others with his inquiries. A quick summary of realism vs idealism:
• George Berkeley asserted that the external world is merely ideas in the mind. He is famous for his “Does a falling tree make a sound if nobody is there to hear it”.
• David Hume, asserted that we can never know what an external world consists of because our knowledge is limited to the ideas in the mind.
• Thomas Reid claimed the foundations upon which our “sensus communis” are built, justify our belief that there is an external world. Common Sense is and should be the basis of all philosophical inquiry.
Here also a background video on direct realism https://www.youtube.com/watch?v=kpTgySxdC14
Most important is his influential book “Inquiry into the Human Mind on the Principles of Common Sense”
See Especially Chapter 6: “Of seeing” and its section 9 “Of the Geometry of Visibles”.
https://books.google.com/books?id=cadgAAAAcAAJ&printsec=frontcover&dq=inauthor:thomas+inauthor:reid&hl=en&sa=X&ved=0ahUKEwiUlO7iwcvNAhUH8RQKHWBfDMgQ6AEIQjAG#v=onepage&q&f=false
This is a must read for everybody. His writing style is detailed, yet lucid. The book contains lots of information relevant to the perception deception. Chapter 6 got me digging deep into maths, geometry, optics and art, uncovering both wilful and accidental deceptions.
Here a quote from another of his books “The intellectual powers of man” to whet your appetite. The quote especially applies to globeheads.
"For, before men can reason together, they must agree in first principles; and it is impossible to reason with a man who has no principles in common with you." One of the first principles he goes on to list is that "qualities must necessarily be in something that is figured, coloured, hard or soft, that moves or resists. It is not to these qualities, but to that which is the subject of them, that we give the name body. If any man should think fit to deny that these things are qualities, or that they require any subject, I leave him to enjoy his opinion as a man who denies first principles, and is not fit to be reasoned with."
2. R.B. Angell, Professor of Philosophy
http://www.rbangell.com/papersAndArticles.asp
A logician, realist and proponent of Reid who throughout his career studied the “Geometry of Visibles” and questioned many mathematical truths and exposed foundations as being logically false.
3. NJ Wildberger (YouTube)
https://www.youtube.com/channel/UCXl0Zbk8_rvjyLwAR-Xh9pQ
A pure mathematician and lecturer with his own YouTube channel and hundreds of videos. A bright and sensible man with great teaching skills in Geometry, and a defender of rational concepts. He would like to re-boot many of areas of mathematics due to the lack of rigor and logical errors.
Here a good primer on non-euclidean geometry (historical overview)
https://www.youtube.com/watch?v=zHh9q_nKrbc&index=22&list=PL55C7C83781CF4316
Most of his presentations are understandable with a high school math background.
Introduction
I’ve started this as a new topic, because it covers a range of things indirectly related to the Flat Earth and difficult to slot into an existing category. In addition, there is background material of a general nature to convey on vision, geometry, philosophy, arts, etc. to (hopefully) make the connections and conclusions clear.
As I approach my 2nd anniversary on the flat earth, I remain intrigued and eager to discover how the deception is/was perpetuated and how it fooled (and continues to fool), so many people. It is clear that the deception is on multiple levels within mathematics, physics, astronomy, geology, archaeology, cosmology, arts, philosophy, language, etc., but there do appear to be key components on which the deception depends.
I think a cornerstone (or capstone ;-) of the deception is concealed in the nature of vision, the laws of optical instruments and certain mathematical theories of geometrical spaces.
Our eyes convey the most important sense data that we receive and are consequently instrumental in shaping our perceptions and beliefs. Hence the obsession of the ruling criminals with the “all-seeing eye” and one-eyed symbolism. I think they are hiding the truth in plain sight.
Before we go into detail, let me try and sum up my conclusion in one paragraph:
We have been deceived into believing, that we possess (Euclidean) vision, incapable of sensing an infinite, non-Euclidean universe. The opposite is true. Our vision is non-Euclidean and we are experiencing a finite Euclidean reality.
I am cautiously aware that the language and terminology used, might not mean the same to everybody (e.g. non-Euclidean) and will try to be as precise as possible.
Many thanks to IFERS and the research and studies of many people, too numerous to mention both dead and alive. I have freely consolidated their ideas with my own research to form the above conclusion.
Knowing that Space, et al. is fake, assisted me greatly when reviewing older manuscripts of smart people and interpreting their theories and insights in a different light. I’m sure some if some of them had known what we know now, they might also have interpreted their findings differently. In that sense, we digital natives have an advantage, since we can exclude interpretations we know to be false, leaving more of the truth exposed.
References can be found by searching the internet and thinking for yourself ;-)
All errors are of my own making.
Some essential and important reference materials.
1. Thomas Reid a Scots Minister, Regent and Natural Philosopher
https://en.wikipedia.org/wiki/Thomas_Reid
https://en.wikipedia.org/wiki/Scottish_Common_Sense_Realism
As a regent, he was an accomplished polymath, but grounded in common sense. In my opinion he wiped the floor with his contemporaries such as Bishop Berkeley, Hume, Locke, Kant and many others with his inquiries. A quick summary of realism vs idealism:
• George Berkeley asserted that the external world is merely ideas in the mind. He is famous for his “Does a falling tree make a sound if nobody is there to hear it”.
• David Hume, asserted that we can never know what an external world consists of because our knowledge is limited to the ideas in the mind.
• Thomas Reid claimed the foundations upon which our “sensus communis” are built, justify our belief that there is an external world. Common Sense is and should be the basis of all philosophical inquiry.
Here also a background video on direct realism https://www.youtube.com/watch?v=kpTgySxdC14
Most important is his influential book “Inquiry into the Human Mind on the Principles of Common Sense”
See Especially Chapter 6: “Of seeing” and its section 9 “Of the Geometry of Visibles”.
https://books.google.com/books?id=cadgAAAAcAAJ&printsec=frontcover&dq=inauthor:thomas+inauthor:reid&hl=en&sa=X&ved=0ahUKEwiUlO7iwcvNAhUH8RQKHWBfDMgQ6AEIQjAG#v=onepage&q&f=false
This is a must read for everybody. His writing style is detailed, yet lucid. The book contains lots of information relevant to the perception deception. Chapter 6 got me digging deep into maths, geometry, optics and art, uncovering both wilful and accidental deceptions.
Here a quote from another of his books “The intellectual powers of man” to whet your appetite. The quote especially applies to globeheads.
"For, before men can reason together, they must agree in first principles; and it is impossible to reason with a man who has no principles in common with you." One of the first principles he goes on to list is that "qualities must necessarily be in something that is figured, coloured, hard or soft, that moves or resists. It is not to these qualities, but to that which is the subject of them, that we give the name body. If any man should think fit to deny that these things are qualities, or that they require any subject, I leave him to enjoy his opinion as a man who denies first principles, and is not fit to be reasoned with."
2. R.B. Angell, Professor of Philosophy
http://www.rbangell.com/papersAndArticles.asp
A logician, realist and proponent of Reid who throughout his career studied the “Geometry of Visibles” and questioned many mathematical truths and exposed foundations as being logically false.
3. NJ Wildberger (YouTube)
https://www.youtube.com/channel/UCXl0Zbk8_rvjyLwAR-Xh9pQ
A pure mathematician and lecturer with his own YouTube channel and hundreds of videos. A bright and sensible man with great teaching skills in Geometry, and a defender of rational concepts. He would like to re-boot many of areas of mathematics due to the lack of rigor and logical errors.
Here a good primer on non-euclidean geometry (historical overview)
https://www.youtube.com/watch?v=zHh9q_nKrbc&index=22&list=PL55C7C83781CF4316
Most of his presentations are understandable with a high school math background.
Last edited by vortexpuppy on Wed Jun 29, 2016 1:10 pm; edited 2 times in total (Reason for editing : broken url)
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
Standswithmic, 0xtehAman and Forest4theTreez like this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Introductory Elements of the deception.
I intend to focus mainly on the vision deception, but before I do, here is an incomplete list of related topics of the ongoing occulting, probably already known to most folks here, but they will help frame what follows:
1. From Natural Philosophy to Scientism
Natural Philosophy was the discipline given to studying the totality of natural sciences. It was the philosophical study of nature and our physical universe. It was basically trying to understand reality and its nature. It was the dominant multi-discipline science for thousands of years, before its splitting and division into “expert” scientific fields. In the 19th century Natural Philosophy was reshaped into the concept of “Science” with re-defined areas such as physics, biology, chemistry, geology, etc.
https://en.wikipedia.org/wiki/Natural_philosophy
Scientism is basically an atheistic materialist philosophy (points, particles, etc.) helping itself to copious portions of idealism and imagination incorporating numerous religious cosmologies (big bang, helio, etc.) with an agenda to dumb-down via an artificial division.
A modern example of this is the infamous hockey stick science data that tried to sell us bullshit climate change, as a way to carbon tax us all and increase the profits of money lenders. It zooms in on a small section of data to sneakily hide the bigger picture.
Scientism is now a fully-fledged religion. It replaced what used to be called Nature, or God, or the creator, the architect, the divine mechanic, or whatever you want to call it (feel free to replace the word “God” with a concept of your own choosing). I, like many others was educated to ridicule such beliefs and blindly believe scientists, all the time thinking that I was being a “modern realist”. The argument typically went something like:
“The deluded, religious faithful just can’t accept the reality that we are insignificant stardust in a godless universe, so they have to clamor and embrace a God or Savior (of a particular religion), to make sense of death and hope for a life after this existence. We scientists have no need of such child-like fantasies”.
However, it is important to see that inquiring (or philosophizing) about / into nature, reality and creation is not the same thing as being of a particular religious’ faith, such as Christianity, Muslim, Hindu, Buddhism, etc.
Up until 2 years ago, I threw out the baby with the bath water, which I guess was their intention all the time.
2. Mathematical absurdities: Zero, Infinity and Incommensurability.
In mathematics, many imaginary concepts have been introduced such as zero, infinity, negative numbers, irrational numbers, etc., all of which have no foundation in reality (see the famous Tesla quote).
In the true definition of Natural numbers there is no zero; there are no negative numbers; no complex imaginary numbers; no incommensurable numbers, no square root, n-roots; no PI; no Sines or Cosines; no power series approximations and no concept of infinity. “Zero” is sometimes added to the natural numbers to make “whole numbers”, but this is just smoke and mirrors. https://en.wikipedia.org/wiki/Natural_number
Zero
Zero is not a natural number. It does not occur in Nature. It is the absence of anything/everything. It does not exist. It should not be “counted” as a natural number, since it cannot be counted. If there is nothing, then there is nothing to talk about.
Zero, when signifying a decimal shift is important to the money lenders, but any other symbol would have worked just as well. Using Zero for decimal places is but a subtle introduction that conditions us to accept Zero as a natural number. Zero was initially thought by some religious Orders to be a device of the devil and there was a lot of resistance but merchants adopted Arabic numerals and zero for calculation, so it was eventually universally received.
(See Robert Lawlor – Sacred Geometry)
Zero is said to have originated in India, around the time, 800 AD, when a new school of thought started in Hinduism (through Shankhara) and Buddhism (through Narayana), that laid exclusive emphasis on the goal of obtaining personal transcendence and escape from karma through renunciation of the natural world, to the extent of mortification of the physical body. This is now considered by many to be a dark period in the rich spiritual heritage of India and a decline from the previous tradition which upheld a spiritual significance in both the manifested and the unmanifested expressions of God.
Adding zero meant that the structure of arithmetic had to be changed. Normally addition of numbers led to a sum larger than either original number. This was nullified when using zero. New operations were introduced such as 3 + 0 = 0 and 3 x 0 = 0 and when 3 / 0 = 0 (???) the logic breaks down and remains undefined to this day.
So treating Zero as a number is a logical fallacy, with no anchor in reality. This in turn allowed the existence of more imaginary numbers and introduced a range of new numerical and symbolical entities with no verifiable concept or geometric form. The invention of zero permitted numbers to represent ideas which have no form. This also led to a change in the definition of the word “idea” which was previously synonymous with form and geometry.
Nowadays, zero is indispensable in mathematics. It has also impacted philosophy and theology and changed our view and attitude towards nature. Zero is associated with a doctrine that negates the reality of the material world. The Sanskrit name for zero, “sunya”, meaning “empty” became “chiffra” in Latin, which means “null or nothing”. Nothing is obviously a different concept than empty. Also the Sanskrit word “maya” took on a new meaning. Originally it meant the “power to divide” or the “dividing mind”, but now it means illusion, or that the material aspect of the universe is an illusion. We see the reverse duality of this in western philosophy, where zero is a framework for the development of atheism and negation of the spiritual.
The impact of Zero was so great that it caused physics of the 19th century to adopt the atomic particle theory, in which matter is modelled as composed of little spheres floating in a zero or empty void. This is basically the same bullshit as the fake space we are sold today.
Infinity
You cannot count to infinity. You can never reach infinity. It never ends, so the final entity “infinity” continually eludes you. You cannot imagine infinity. Nobody can.
Some people maintain that they can imagine infinity. In reality, they are only imagining themselves, imagining infinity. This also applies to the concept of “infinite space” or “infinite void”, the holes left behind by the absence of any material Objects. It is impossible to imagine an infinite universe or an infinite anything.
Square roots were first called “unutterables”, since it is not possible to name them distinctly like we can with one, two, and three. The square root of two is an irrational number that starts with 1.41421356723… and continues for ever to “infinity”. Two real numbers a and b are said to be incommensurable when a/b is an irrational number.
Calculating a Sine or Cosine, a square root or PI, is done by approximating an infinite power series. They go on forever. You stop adding the terms of the series at the required “precision of measurement” and this is then the approximated value that is used. It can never be calculated exactly, since it would necessitate infinite time and energy to calculate a never-ending power series, which is absurd to reason and common sense. So the angle values are but approximations of a number that can never be accurately calculated or named.
The rational numbers are correctly defined as the Natural numbers together with their multiplicative inverse. A rational number is n, such that: n is a positive integer number 1, 2, 3, …n… or its multiplicative inverse 1/n, such as the fractions ½, ¼, etc.
Rational numbers centred on Unity (One) is the number system used in nature. Numbers such as 1/10, 1/5, 1/3, ½, 1, 2, 3, 5 and 10, form real leaf patterns of trees in nature, whereas -10, -5, -3,-2,-1, 0, 1, 2, 3, 5, 10 has abstract non-existent entities, absurd logic and a discontinuity or an artificial divide at zero.
When thinking purely rational, all this nonsense is removed. We will avoid abstract concepts and inquire further using only finite concepts of ratio and proportionality that are rooted in reality.
For more insights as to where mathematics has problems see also:
Logical weakness in modern pure mathematics
https://www.youtube.com/user/njwildberger/search?query=mf87
3. Dimensions, Measures and Units
For thousands of years, our ancestors used rational concepts in geometry, arithmetic, astronomy, music, etc., the holistic study of natural patterns, using proportions and ratios.
Sure, there were specific measures and units used, but these were all in relation to real finite entities, such as comparing distances with feet, hands, fingers, strides, etc., or comparing weights and densities using real physical objects such as a sack of grain or a heap of wood, etc.
Up until a few hundred years ago, a normal city/town typically had a toll gate and a weighing machine at the entry point, for comparing items that were to be commercially traded. If you wanted to sell a sack of grain, it got compared to a “town standard sack of grain” and you were paid according to the ratio of your sack to their sack.
This is how weight together with the density of the (specific solid, liquid or gas) material was used to compare and measure stuff. You did not compare a sack of rice with a bag of feathers.
Nowadays we have units continuously changing and adapting to suit specific needs and constants introduced to avoid the rational dimensionless proportions. Remember, a ratio or proportion is simply a number fraction and has no unit or dimensions.
Equating F=ma with F=GMm/r2 is an example of this trickery, where dimensionless quantities are obfuscated using constants (G= Gravitational constant) and two separate concepts are made out to be one and the same thing.
Note that any Physical Law must necessarily be a rational concept, irrespective of constants, units or dimensions. For example, Boyle’s Law that pressure is inversely related to volume at a given temperature is mathematically expressed as P is proportional to 1/V. Distance travelled is in a ratio to Speed in a given time, so D is proportional to S. These are true rational statements, whatever units, dimensions or constants are used. To say a physical law exists and is true, is simply to demonstrate a proportionality.
For more insights on this:
Absolute versus relative measurements in geometry
https://www.youtube.com/watch?v=_c5v14ZIUO0
I intend to focus mainly on the vision deception, but before I do, here is an incomplete list of related topics of the ongoing occulting, probably already known to most folks here, but they will help frame what follows:
1. From Natural Philosophy to Scientism
Natural Philosophy was the discipline given to studying the totality of natural sciences. It was the philosophical study of nature and our physical universe. It was basically trying to understand reality and its nature. It was the dominant multi-discipline science for thousands of years, before its splitting and division into “expert” scientific fields. In the 19th century Natural Philosophy was reshaped into the concept of “Science” with re-defined areas such as physics, biology, chemistry, geology, etc.
https://en.wikipedia.org/wiki/Natural_philosophy
Scientism is basically an atheistic materialist philosophy (points, particles, etc.) helping itself to copious portions of idealism and imagination incorporating numerous religious cosmologies (big bang, helio, etc.) with an agenda to dumb-down via an artificial division.
A modern example of this is the infamous hockey stick science data that tried to sell us bullshit climate change, as a way to carbon tax us all and increase the profits of money lenders. It zooms in on a small section of data to sneakily hide the bigger picture.
Scientism is now a fully-fledged religion. It replaced what used to be called Nature, or God, or the creator, the architect, the divine mechanic, or whatever you want to call it (feel free to replace the word “God” with a concept of your own choosing). I, like many others was educated to ridicule such beliefs and blindly believe scientists, all the time thinking that I was being a “modern realist”. The argument typically went something like:
“The deluded, religious faithful just can’t accept the reality that we are insignificant stardust in a godless universe, so they have to clamor and embrace a God or Savior (of a particular religion), to make sense of death and hope for a life after this existence. We scientists have no need of such child-like fantasies”.
However, it is important to see that inquiring (or philosophizing) about / into nature, reality and creation is not the same thing as being of a particular religious’ faith, such as Christianity, Muslim, Hindu, Buddhism, etc.
Up until 2 years ago, I threw out the baby with the bath water, which I guess was their intention all the time.
2. Mathematical absurdities: Zero, Infinity and Incommensurability.
In mathematics, many imaginary concepts have been introduced such as zero, infinity, negative numbers, irrational numbers, etc., all of which have no foundation in reality (see the famous Tesla quote).
In the true definition of Natural numbers there is no zero; there are no negative numbers; no complex imaginary numbers; no incommensurable numbers, no square root, n-roots; no PI; no Sines or Cosines; no power series approximations and no concept of infinity. “Zero” is sometimes added to the natural numbers to make “whole numbers”, but this is just smoke and mirrors. https://en.wikipedia.org/wiki/Natural_number
Zero
Zero is not a natural number. It does not occur in Nature. It is the absence of anything/everything. It does not exist. It should not be “counted” as a natural number, since it cannot be counted. If there is nothing, then there is nothing to talk about.
Zero, when signifying a decimal shift is important to the money lenders, but any other symbol would have worked just as well. Using Zero for decimal places is but a subtle introduction that conditions us to accept Zero as a natural number. Zero was initially thought by some religious Orders to be a device of the devil and there was a lot of resistance but merchants adopted Arabic numerals and zero for calculation, so it was eventually universally received.
(See Robert Lawlor – Sacred Geometry)
Zero is said to have originated in India, around the time, 800 AD, when a new school of thought started in Hinduism (through Shankhara) and Buddhism (through Narayana), that laid exclusive emphasis on the goal of obtaining personal transcendence and escape from karma through renunciation of the natural world, to the extent of mortification of the physical body. This is now considered by many to be a dark period in the rich spiritual heritage of India and a decline from the previous tradition which upheld a spiritual significance in both the manifested and the unmanifested expressions of God.
Adding zero meant that the structure of arithmetic had to be changed. Normally addition of numbers led to a sum larger than either original number. This was nullified when using zero. New operations were introduced such as 3 + 0 = 0 and 3 x 0 = 0 and when 3 / 0 = 0 (???) the logic breaks down and remains undefined to this day.
So treating Zero as a number is a logical fallacy, with no anchor in reality. This in turn allowed the existence of more imaginary numbers and introduced a range of new numerical and symbolical entities with no verifiable concept or geometric form. The invention of zero permitted numbers to represent ideas which have no form. This also led to a change in the definition of the word “idea” which was previously synonymous with form and geometry.
Nowadays, zero is indispensable in mathematics. It has also impacted philosophy and theology and changed our view and attitude towards nature. Zero is associated with a doctrine that negates the reality of the material world. The Sanskrit name for zero, “sunya”, meaning “empty” became “chiffra” in Latin, which means “null or nothing”. Nothing is obviously a different concept than empty. Also the Sanskrit word “maya” took on a new meaning. Originally it meant the “power to divide” or the “dividing mind”, but now it means illusion, or that the material aspect of the universe is an illusion. We see the reverse duality of this in western philosophy, where zero is a framework for the development of atheism and negation of the spiritual.
The impact of Zero was so great that it caused physics of the 19th century to adopt the atomic particle theory, in which matter is modelled as composed of little spheres floating in a zero or empty void. This is basically the same bullshit as the fake space we are sold today.
Infinity
You cannot count to infinity. You can never reach infinity. It never ends, so the final entity “infinity” continually eludes you. You cannot imagine infinity. Nobody can.
Some people maintain that they can imagine infinity. In reality, they are only imagining themselves, imagining infinity. This also applies to the concept of “infinite space” or “infinite void”, the holes left behind by the absence of any material Objects. It is impossible to imagine an infinite universe or an infinite anything.
Square roots were first called “unutterables”, since it is not possible to name them distinctly like we can with one, two, and three. The square root of two is an irrational number that starts with 1.41421356723… and continues for ever to “infinity”. Two real numbers a and b are said to be incommensurable when a/b is an irrational number.
Calculating a Sine or Cosine, a square root or PI, is done by approximating an infinite power series. They go on forever. You stop adding the terms of the series at the required “precision of measurement” and this is then the approximated value that is used. It can never be calculated exactly, since it would necessitate infinite time and energy to calculate a never-ending power series, which is absurd to reason and common sense. So the angle values are but approximations of a number that can never be accurately calculated or named.
The rational numbers are correctly defined as the Natural numbers together with their multiplicative inverse. A rational number is n, such that: n is a positive integer number 1, 2, 3, …n… or its multiplicative inverse 1/n, such as the fractions ½, ¼, etc.
Rational numbers centred on Unity (One) is the number system used in nature. Numbers such as 1/10, 1/5, 1/3, ½, 1, 2, 3, 5 and 10, form real leaf patterns of trees in nature, whereas -10, -5, -3,-2,-1, 0, 1, 2, 3, 5, 10 has abstract non-existent entities, absurd logic and a discontinuity or an artificial divide at zero.
When thinking purely rational, all this nonsense is removed. We will avoid abstract concepts and inquire further using only finite concepts of ratio and proportionality that are rooted in reality.
For more insights as to where mathematics has problems see also:
Logical weakness in modern pure mathematics
https://www.youtube.com/user/njwildberger/search?query=mf87
3. Dimensions, Measures and Units
For thousands of years, our ancestors used rational concepts in geometry, arithmetic, astronomy, music, etc., the holistic study of natural patterns, using proportions and ratios.
Sure, there were specific measures and units used, but these were all in relation to real finite entities, such as comparing distances with feet, hands, fingers, strides, etc., or comparing weights and densities using real physical objects such as a sack of grain or a heap of wood, etc.
Up until a few hundred years ago, a normal city/town typically had a toll gate and a weighing machine at the entry point, for comparing items that were to be commercially traded. If you wanted to sell a sack of grain, it got compared to a “town standard sack of grain” and you were paid according to the ratio of your sack to their sack.
This is how weight together with the density of the (specific solid, liquid or gas) material was used to compare and measure stuff. You did not compare a sack of rice with a bag of feathers.
Nowadays we have units continuously changing and adapting to suit specific needs and constants introduced to avoid the rational dimensionless proportions. Remember, a ratio or proportion is simply a number fraction and has no unit or dimensions.
Equating F=ma with F=GMm/r2 is an example of this trickery, where dimensionless quantities are obfuscated using constants (G= Gravitational constant) and two separate concepts are made out to be one and the same thing.
Note that any Physical Law must necessarily be a rational concept, irrespective of constants, units or dimensions. For example, Boyle’s Law that pressure is inversely related to volume at a given temperature is mathematically expressed as P is proportional to 1/V. Distance travelled is in a ratio to Speed in a given time, so D is proportional to S. These are true rational statements, whatever units, dimensions or constants are used. To say a physical law exists and is true, is simply to demonstrate a proportionality.
For more insights on this:
Absolute versus relative measurements in geometry
https://www.youtube.com/watch?v=_c5v14ZIUO0
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
0xtehAman and Forest4theTreez like this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
4. Geometry
Geometries have been created and redefined with inventive axioms using infinity and parallels, that model unseen higher dimensional realms definitions. Branches of Geometry have been re-named or subsumed under different areas adding to the difficulty of differentiating theories and definitions.
Perspective Geometry has been replaced by projective geometry, a beautiful science in itself, but one in which Euclidean concepts of parallel lines are ignored or modified, so that it is barely comprehensible, even to mathematicians.
Hyperbolic and projective geometries can create weird imaginative, unverifiable universes, where space-time is curved, measuring rods contract and where clocks run slower or faster at light speeds. These are fantasies of science fiction begging credulity, lacking honest witness and by their own admission unverifiable, since it’s the same in every “frame of reference”.
Spherical geometry is easily confused with the mathematical meaning of non-Euclidean Geometry, although Euclidean geometry already includes the treatment of spheres and conics. For example, the Euclidean book “Sphaerica” by Theodosius which deals geometrically with matters of relevance to astronomy. Sphaerica was standard reading when astronomy, astrology and the associated mathematics were taught in Greece, Persia, Islamic, Jewish and European universities.
It taught the plane, solid and spherical geometry, planetary models and the calculation of stellar positions. It didn’t solve higher practical astronomical problems, such as finding the nightly hours from stellar positions. This needs trigonometry. Enter Hipparchus who calculated a table of chords. On this basis, ratios between spherical arcs could be calculated and distances could be determined. The accuracy and predictability given by Euclid and Sphaerica ensured their survival in geometry and astronomy books for 1500 years.
In current mathematical geometry, there is a distinction between a Sphere and a Ball. The Sphere is a 2 Dimensional closed surface embedded in 3D Euclidean Space. It is usually the surface of a 3D Object existing in our Euclidean reality, such as a ball or cube. A mathematical Ball is defined to be a 3D Object that includes the Sphere, aka the surface, as well as everything inside the Ball.
We are also taught that Spherical geometry is the geometry of the 2D surface of a Sphere and that it is an example of a geometry that is non-Euclidean.
Now two practical proven examples of spherical geometry are navigation and astronomy and they certainly work. It was known to ancient mariners and astronomers and astrologists for thousands of years. They use(d) the “Celestial Sphere”, with the Earth as the center of concentric, 3D rotatable spherical shell(s) in the paths of which, luminaries could orbit, creating distinct predictable figures and patterns “measureable” on the Sphere.
Why then is Spherical Geometry said to be non-Euclidean if it has been part of accepted Euclidean teachings for a long time? Well that depends on your definitions and axioms and there’s more than enough of them to go round and round ;-)
What were they measuring exactly? Our inquiry into geometric space, its beauty and truth, as well as its misuse and abuse, is just getting started.
Geometries have been created and redefined with inventive axioms using infinity and parallels, that model unseen higher dimensional realms definitions. Branches of Geometry have been re-named or subsumed under different areas adding to the difficulty of differentiating theories and definitions.
Perspective Geometry has been replaced by projective geometry, a beautiful science in itself, but one in which Euclidean concepts of parallel lines are ignored or modified, so that it is barely comprehensible, even to mathematicians.
Hyperbolic and projective geometries can create weird imaginative, unverifiable universes, where space-time is curved, measuring rods contract and where clocks run slower or faster at light speeds. These are fantasies of science fiction begging credulity, lacking honest witness and by their own admission unverifiable, since it’s the same in every “frame of reference”.
Spherical geometry is easily confused with the mathematical meaning of non-Euclidean Geometry, although Euclidean geometry already includes the treatment of spheres and conics. For example, the Euclidean book “Sphaerica” by Theodosius which deals geometrically with matters of relevance to astronomy. Sphaerica was standard reading when astronomy, astrology and the associated mathematics were taught in Greece, Persia, Islamic, Jewish and European universities.
It taught the plane, solid and spherical geometry, planetary models and the calculation of stellar positions. It didn’t solve higher practical astronomical problems, such as finding the nightly hours from stellar positions. This needs trigonometry. Enter Hipparchus who calculated a table of chords. On this basis, ratios between spherical arcs could be calculated and distances could be determined. The accuracy and predictability given by Euclid and Sphaerica ensured their survival in geometry and astronomy books for 1500 years.
In current mathematical geometry, there is a distinction between a Sphere and a Ball. The Sphere is a 2 Dimensional closed surface embedded in 3D Euclidean Space. It is usually the surface of a 3D Object existing in our Euclidean reality, such as a ball or cube. A mathematical Ball is defined to be a 3D Object that includes the Sphere, aka the surface, as well as everything inside the Ball.
We are also taught that Spherical geometry is the geometry of the 2D surface of a Sphere and that it is an example of a geometry that is non-Euclidean.
Now two practical proven examples of spherical geometry are navigation and astronomy and they certainly work. It was known to ancient mariners and astronomers and astrologists for thousands of years. They use(d) the “Celestial Sphere”, with the Earth as the center of concentric, 3D rotatable spherical shell(s) in the paths of which, luminaries could orbit, creating distinct predictable figures and patterns “measureable” on the Sphere.
Why then is Spherical Geometry said to be non-Euclidean if it has been part of accepted Euclidean teachings for a long time? Well that depends on your definitions and axioms and there’s more than enough of them to go round and round ;-)
What were they measuring exactly? Our inquiry into geometric space, its beauty and truth, as well as its misuse and abuse, is just getting started.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
0xtehAman and Forest4theTreez like this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Great research and analysis VP, thanks for sharing!
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
5. Perspective Art & Psychology
We now use the words “perspective” to mean many different things.
Similar to how “legalese” willfully manipulates the language of law, to solicit contracts and promote usury, so too have geometric definitions and many words including “perspective” been divided, doubled and diluted in myriad ways by deceitful language, so as to be nearly useless in debates and discussions. The meaning and common ground under our feet has been removed.
Perspective Art
Perspective in addition to becoming projective, has been moved over to the domains of Art and Psychology instead of remaining an exact science based on the laws of geometrical optics.
Art and perspective painting influence our visual perception and can change attitudes and beliefs overnight with symbols and signs in plain sight, yet occulted as to be invisible to our attention. “Signs and symbols rule the world, not words nor laws.” –Confucius
Art has an enormous influence on popular culture as seen by the renaissance periods, by suspiciously weird painters such as Escher, (e.g. Circle of Limits), Salvador Dali, or more modern phenomena such as Andy Warhol with Pop art & Advertising. Flower power and other such movements we know to be controlled opposition and their associated Art plays a role in anchoring beliefs and creating specific perceptions in our minds. Critics and art historians assist (whether willful or inadvertent) in re-defining our “visible signs and triggers” to fit manipulative agendas.
Our perceptions, induced via visible signs and triggers, are constantly wiped or replaced and always outnumbered by their signs and symbols. At an early age we are ready to be programmed to think what they want us to think, to perceive what they want us to perceive, to see what they want us to see. Whenever you see the sign or symbol you think automatically of the end result, without even realizing it. You pass over the visible sign without seeing it because you pay it no attention.
In perspective art, typically an Eye or a Camera is situated at a specific point of view. However, the picture or photo - whether printed on paper or viewed on a computer screen - that is produced by the camera (or artist) by reflecting onto a vertical plane, is only a plane Representation of the visual image and not the real visible entity seen by the Eye.
Representations of Objects on canvas, paper, screens are not what we see in real life. In fact, it is known that a good artist rather tries to paint the “signs” that the Eye will receive and that are the trigger to invoke a specific image in an observers’ mind. The observer will not necessarily be aware that this is happening. This image in the Observers mind is what the artist wanted to trigger all along. The brush strokes and colors on canvas are not painting the final image, but creating a picture that will be processed by an optical instrument and will invoke the desired image of which the picture is a sign. The final image in your mind, your perception, is one thing, but the signs that were given to the Eye were different.
You pay these signs no attention, similar to the way Stage hypnotists can get you to do or say things by dividing or distracting your attention from your actions.
Psychology
Psychologists tell us that we see with our mind and that it can be easily deceived. That we are deceived is certainly true as we all know, but that seeing is all in the mind is proverbial horse-feathers and is not confirmed by common sense and reason.
In focusing their attention purely on the results of the mind or the judgements made by the mind in optical illusions (e.g. controversy on the so-called moon illusion), they ignore the workings and nature of light and vision. They generally do not analyze or understand the optical instrument involved - the amazing sense organ we call the Eye - or the environment in which it experiences light.
The visual cliff experiment (Gibson and Walk, 1960) is a good insight into the nature of vision and psychology where mothers try to get their infants to walk over a visual cliff. Infants will sense danger and experience uncertainty, suspending their natural born credulity to believe adults and in particular their mother.
https://www.youtube.com/watch?v=WanGt1G6ScA
https://www.youtube.com/watch?v=3WvtEFJGp-8
Nature seems to protects us both ways. As infants we trust adults to do the right things and are confirmed when they do nurture and protect us. However, Nature also stops us ignoring a situation with contrary sense data from vision and touch. We are uncertain, hesitate and stay out of danger. We believe our eyes more than anything else.
This is only a tiny part of the information available on these subject and serves at this stage only to frame Perspective Art and Psychology as elements of the deception. More on these topics soon.
Important is to realize that a picture representation on a plane is not the same as what your Eyes see in real-time and that perspective art is enmeshed with our experience and understanding of geometrical spaces.
We must be very discerning about what is often represented as geometrical proof about our reality in the flat vs globe debate. When we are shown physical objects, drawn with a lead pencil, of lines and circles, on a flat piece of paper on a table or canvas that exists in 3D-Euclidean space, then it only proves that these drawn entities conform to the relationships of Euclidean geometry (or to a specific projection e.g. parallel projection). These so called proofs do not show what is actually presented to the Eye at a particular instant in time, from a particular position or situation of the Eye and do not address the geometry of visible space.
We now use the words “perspective” to mean many different things.
Similar to how “legalese” willfully manipulates the language of law, to solicit contracts and promote usury, so too have geometric definitions and many words including “perspective” been divided, doubled and diluted in myriad ways by deceitful language, so as to be nearly useless in debates and discussions. The meaning and common ground under our feet has been removed.
Perspective Art
Perspective in addition to becoming projective, has been moved over to the domains of Art and Psychology instead of remaining an exact science based on the laws of geometrical optics.
Art and perspective painting influence our visual perception and can change attitudes and beliefs overnight with symbols and signs in plain sight, yet occulted as to be invisible to our attention. “Signs and symbols rule the world, not words nor laws.” –Confucius
Art has an enormous influence on popular culture as seen by the renaissance periods, by suspiciously weird painters such as Escher, (e.g. Circle of Limits), Salvador Dali, or more modern phenomena such as Andy Warhol with Pop art & Advertising. Flower power and other such movements we know to be controlled opposition and their associated Art plays a role in anchoring beliefs and creating specific perceptions in our minds. Critics and art historians assist (whether willful or inadvertent) in re-defining our “visible signs and triggers” to fit manipulative agendas.
Our perceptions, induced via visible signs and triggers, are constantly wiped or replaced and always outnumbered by their signs and symbols. At an early age we are ready to be programmed to think what they want us to think, to perceive what they want us to perceive, to see what they want us to see. Whenever you see the sign or symbol you think automatically of the end result, without even realizing it. You pass over the visible sign without seeing it because you pay it no attention.
In perspective art, typically an Eye or a Camera is situated at a specific point of view. However, the picture or photo - whether printed on paper or viewed on a computer screen - that is produced by the camera (or artist) by reflecting onto a vertical plane, is only a plane Representation of the visual image and not the real visible entity seen by the Eye.
Representations of Objects on canvas, paper, screens are not what we see in real life. In fact, it is known that a good artist rather tries to paint the “signs” that the Eye will receive and that are the trigger to invoke a specific image in an observers’ mind. The observer will not necessarily be aware that this is happening. This image in the Observers mind is what the artist wanted to trigger all along. The brush strokes and colors on canvas are not painting the final image, but creating a picture that will be processed by an optical instrument and will invoke the desired image of which the picture is a sign. The final image in your mind, your perception, is one thing, but the signs that were given to the Eye were different.
You pay these signs no attention, similar to the way Stage hypnotists can get you to do or say things by dividing or distracting your attention from your actions.
Psychology
Psychologists tell us that we see with our mind and that it can be easily deceived. That we are deceived is certainly true as we all know, but that seeing is all in the mind is proverbial horse-feathers and is not confirmed by common sense and reason.
In focusing their attention purely on the results of the mind or the judgements made by the mind in optical illusions (e.g. controversy on the so-called moon illusion), they ignore the workings and nature of light and vision. They generally do not analyze or understand the optical instrument involved - the amazing sense organ we call the Eye - or the environment in which it experiences light.
The visual cliff experiment (Gibson and Walk, 1960) is a good insight into the nature of vision and psychology where mothers try to get their infants to walk over a visual cliff. Infants will sense danger and experience uncertainty, suspending their natural born credulity to believe adults and in particular their mother.
https://www.youtube.com/watch?v=WanGt1G6ScA
https://www.youtube.com/watch?v=3WvtEFJGp-8
Nature seems to protects us both ways. As infants we trust adults to do the right things and are confirmed when they do nurture and protect us. However, Nature also stops us ignoring a situation with contrary sense data from vision and touch. We are uncertain, hesitate and stay out of danger. We believe our eyes more than anything else.
This is only a tiny part of the information available on these subject and serves at this stage only to frame Perspective Art and Psychology as elements of the deception. More on these topics soon.
Important is to realize that a picture representation on a plane is not the same as what your Eyes see in real-time and that perspective art is enmeshed with our experience and understanding of geometrical spaces.
We must be very discerning about what is often represented as geometrical proof about our reality in the flat vs globe debate. When we are shown physical objects, drawn with a lead pencil, of lines and circles, on a flat piece of paper on a table or canvas that exists in 3D-Euclidean space, then it only proves that these drawn entities conform to the relationships of Euclidean geometry (or to a specific projection e.g. parallel projection). These so called proofs do not show what is actually presented to the Eye at a particular instant in time, from a particular position or situation of the Eye and do not address the geometry of visible space.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
Forest4theTreez likes this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
6. Philosophy & Common Sense
A parallel philosophical debate that has also raged for thousands of years is the one concerning the nature of reality but now philosophy has been separated from Natural Studies and wears a straightjacket (or cardigan) smoking a pipe and sitting in an armchair.
Philosophy has abandoned zetetic inquiry and empirical evidence. In pursuit of knowledge, it depends mostly on thought experiments riddled with logical errors. In doing so it has abandoned reason and common sense, just as mathematics and natural sciences have distanced themselves from reality.
There are notable exceptions such as Thomas Reid and others as mentioned in the introduction. We will get back to them again soon.
Common Sense
I cannot possibly do justice to Thomas Reid in trying to summarize his works, but will start with what I think common sense really means.
Common sense is about correlating different senses (vision, touch, smell, hearing, tasting) to give us an overall understanding of reality. It is something we learn most as children and as adults we don’t remember how we did it.
Common Sense is also something we have in common with others, so that when many people have a “common sense” it helps us decide what is real and what is fantasy or just stories.
Nature has been wise to give us senses that can correlate. We comprehend when the different senses get together and collectively confirm patterns and impressions in nature.
We learn as children to stop futile grasps at the moon, but learn to smell, reach, touch, throw stuff in a cot, then crawl, walk, run in a playpen, then a room, etc.
As an infant we see visible signs, much more so than as adults. We go from 4-6 weeks “blindness” to a kind of kaleidoscope-like visual field of figures and colors. You do not “see” these visible figures anymore as an adult. You have already correlated these with your other senses, touched them with your feet and hands, smelt the wooden frame of your cot, heard the knocking sound on the floor, in direct correspondence to the finite Euclidean world around you. You have with your hands, feet, strides measured your local world and aligned these findings with your visual impressions.
Now you give little or no attention to what you “see” when you grab a cup of coffee from the table. A quick look is immediately passed over into the action of your arm reaching for the cup. But what did you actually see?
We have difficulty in actually attending to the images before us. We all pass swiftly past the image which is taken merely as a sign of the actual figure of the object of perception.
In comparing the two senses of touch and vision, Reid argues (and I am fully convinced and hope to show this) that the geometry of space that everyone learns in school is in fact a geometry of touch and that the geometry of visible objects is different!
Reid argues convincingly that the geometry of the objects of vision has “entirely escaped the notice of mathematicians” and “while that figure and that extension which are objects of touch, have been tortured ten thousand ways for twenty centuries, [...] not a single proposition do we find with regard to the figure and extension which are the immediate objects of sight”.
We are not correctly informed (or not informed at all) about how our vision works and how illuminated objects are seen and/or perceived. The geometry of optics and vision has been hijacked by the same den of thieves (e.g. Pythagoras, Kepler, Newton, Copernicus, Galileo, Einstein, etc.) who invented optical instruments, our modern cosmologies, spherical spinning globes, heliocentric models and numerous applied mathematical concepts such as the craftily worded gravitational “lens” equations.
By using common sense I hope everybody can wake up to the monumental deception
A parallel philosophical debate that has also raged for thousands of years is the one concerning the nature of reality but now philosophy has been separated from Natural Studies and wears a straightjacket (or cardigan) smoking a pipe and sitting in an armchair.
Philosophy has abandoned zetetic inquiry and empirical evidence. In pursuit of knowledge, it depends mostly on thought experiments riddled with logical errors. In doing so it has abandoned reason and common sense, just as mathematics and natural sciences have distanced themselves from reality.
There are notable exceptions such as Thomas Reid and others as mentioned in the introduction. We will get back to them again soon.
Common Sense
I cannot possibly do justice to Thomas Reid in trying to summarize his works, but will start with what I think common sense really means.
Common sense is about correlating different senses (vision, touch, smell, hearing, tasting) to give us an overall understanding of reality. It is something we learn most as children and as adults we don’t remember how we did it.
Common Sense is also something we have in common with others, so that when many people have a “common sense” it helps us decide what is real and what is fantasy or just stories.
Nature has been wise to give us senses that can correlate. We comprehend when the different senses get together and collectively confirm patterns and impressions in nature.
We learn as children to stop futile grasps at the moon, but learn to smell, reach, touch, throw stuff in a cot, then crawl, walk, run in a playpen, then a room, etc.
As an infant we see visible signs, much more so than as adults. We go from 4-6 weeks “blindness” to a kind of kaleidoscope-like visual field of figures and colors. You do not “see” these visible figures anymore as an adult. You have already correlated these with your other senses, touched them with your feet and hands, smelt the wooden frame of your cot, heard the knocking sound on the floor, in direct correspondence to the finite Euclidean world around you. You have with your hands, feet, strides measured your local world and aligned these findings with your visual impressions.
Now you give little or no attention to what you “see” when you grab a cup of coffee from the table. A quick look is immediately passed over into the action of your arm reaching for the cup. But what did you actually see?
We have difficulty in actually attending to the images before us. We all pass swiftly past the image which is taken merely as a sign of the actual figure of the object of perception.
In comparing the two senses of touch and vision, Reid argues (and I am fully convinced and hope to show this) that the geometry of space that everyone learns in school is in fact a geometry of touch and that the geometry of visible objects is different!
Reid argues convincingly that the geometry of the objects of vision has “entirely escaped the notice of mathematicians” and “while that figure and that extension which are objects of touch, have been tortured ten thousand ways for twenty centuries, [...] not a single proposition do we find with regard to the figure and extension which are the immediate objects of sight”.
We are not correctly informed (or not informed at all) about how our vision works and how illuminated objects are seen and/or perceived. The geometry of optics and vision has been hijacked by the same den of thieves (e.g. Pythagoras, Kepler, Newton, Copernicus, Galileo, Einstein, etc.) who invented optical instruments, our modern cosmologies, spherical spinning globes, heliocentric models and numerous applied mathematical concepts such as the craftily worded gravitational “lens” equations.
By using common sense I hope everybody can wake up to the monumental deception
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Intermediary Summary:
There is still much to convey, and I will try to show the overall train of thought that led me to the conclusion, but first a little intermediary summary.
The Eye plays a major role in sensing our 3D Euclidean existence, together with the other senses called touch, sound, taste and smell. It is the Eye gathering data like an optical instrument, that we must differentiate carefully from what “comes to mind”.
With vision it is imperative to understand that there is an intermediary stage and process at work, that we do not control and is not of our own volition. There is a forgotten and now nearly invisible step, that happens when we look at a real physical object in 3D Euclidean space, but before the image of that object, instantly comes into our minds.
We think these two steps are directly connected and we think that this is what the Eye is actually seeing, but it is not. These images, that come instantly in the mind, are not what is actually being seen as “visible to the Eye”. The Eye is seeing intermediary visible Objects (called visibles by Reid) and their associated shapes, figures and colors.
The underlying geometry of these visible figures & shapes, that the Eye actually sees is very different from Euclidean geometry. This geometry underlies our Direct Vision and rightly includes the branch of Optics known as Perspective. Direct Vision shows us that the Eye registers visible objects, as if it were at the center of a sphere looking outwards and viewing the object on the inner concave surface of a sphere.
This is the foundation of the deception / confusion and the reason why mathematics / astronomy / navigation, appear to hold true in dual systems. This is why the Celestial Sphere works for thousands of years. If you replace the Earth at the center of this model with your Eye, (and kind of think of your eye-lid as the projection surface), then the theories work and for the most part hold true.
If you like, the non-Euclidean geometry of an Eye’s direct vision capabilities, has been “removed from the Eye”, and replaced by Euclidean concepts. We are then led to believe that the Eye sees in picture representations on a plane, and that the retina is like a plane surface. If you like, the “curve” of the eye has been placed outside the Eye and we are then told that this is the spherical ball world we live on.
So instead of non-Euclidean vision perceiving a Euclidean reality, we are led to believe we have Euclidean vision perceiving a non-Euclidean universe.
Note that in referring to Euclidean / Non- Euclidean, I am using the mathematical distinction, even though spherical geometry should really be considered part of Euclidean teaching.
There is still much to convey, and I will try to show the overall train of thought that led me to the conclusion, but first a little intermediary summary.
The Eye plays a major role in sensing our 3D Euclidean existence, together with the other senses called touch, sound, taste and smell. It is the Eye gathering data like an optical instrument, that we must differentiate carefully from what “comes to mind”.
With vision it is imperative to understand that there is an intermediary stage and process at work, that we do not control and is not of our own volition. There is a forgotten and now nearly invisible step, that happens when we look at a real physical object in 3D Euclidean space, but before the image of that object, instantly comes into our minds.
We think these two steps are directly connected and we think that this is what the Eye is actually seeing, but it is not. These images, that come instantly in the mind, are not what is actually being seen as “visible to the Eye”. The Eye is seeing intermediary visible Objects (called visibles by Reid) and their associated shapes, figures and colors.
The underlying geometry of these visible figures & shapes, that the Eye actually sees is very different from Euclidean geometry. This geometry underlies our Direct Vision and rightly includes the branch of Optics known as Perspective. Direct Vision shows us that the Eye registers visible objects, as if it were at the center of a sphere looking outwards and viewing the object on the inner concave surface of a sphere.
This is the foundation of the deception / confusion and the reason why mathematics / astronomy / navigation, appear to hold true in dual systems. This is why the Celestial Sphere works for thousands of years. If you replace the Earth at the center of this model with your Eye, (and kind of think of your eye-lid as the projection surface), then the theories work and for the most part hold true.
If you like, the non-Euclidean geometry of an Eye’s direct vision capabilities, has been “removed from the Eye”, and replaced by Euclidean concepts. We are then led to believe that the Eye sees in picture representations on a plane, and that the retina is like a plane surface. If you like, the “curve” of the eye has been placed outside the Eye and we are then told that this is the spherical ball world we live on.
So instead of non-Euclidean vision perceiving a Euclidean reality, we are led to believe we have Euclidean vision perceiving a non-Euclidean universe.
Note that in referring to Euclidean / Non- Euclidean, I am using the mathematical distinction, even though spherical geometry should really be considered part of Euclidean teaching.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
Forest4theTreez likes this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Introducing Thomas Reid and the Geometry of Visibles.
Here are important extracts from the aforementioned book on the Geometry of visibles. This shows why Reids visual geometry can be considered “non-euclidean” as per the currently accepted definitions. The rest of this post are Reid own words.
In this geometry, the definitions of a point of a line, whether straight or curve ; of an angle, whether acute, or right, or obtuse; and of a circle are the same as in common geometry. The mathematical reader will easily enter into the whole mystery of this geometry, if he attends duly to these few evident principles.
1. Supposing the eye placed in the centre of a sphere, every great circle of the sphere will have the same appearance to the eye as if it was a straight line; for the curvature of the circle being turned directly toward the eye, is not perceived by it. And, for the same reason,
any line which is drawn in the plane of a great circle of the sphere, whether it be in reality straight or curve, will appear straight to the eye.
2. Every visible right line will appear to coincide with some great circle of the sphere; and the circumference of that great circle, even when it is produced until it returns into itself, will appear to be a continuation of the same visible right line, all the parts of it being visibly in directum. For the eye, perceiving only the position of objects with regard to itself, and not their distance, will see those points in the same visible place which have the same position with regard to the eye, however different their distances from it may be. Now, since a plane passing through the eye and a given visible right line, will be the plane of some great circle
of the sphere, every point of the visible right line will have the same position as some point of the great circle; therefore, they will both have the same visible place, and coincide to the eye; and the whole circumference of the great circle, continued even until it returns into itself, will appear to be a continuation of the same visible right line.
Hence it follows
3. That every visible right line, when it is continued in directum, as far as it may be continued, will be represented by a great circle of a sphere, in whose centre the eye is placed. It follows
4. That the visible angle comprehended under two visible right lines, is equal to the spherical angle comprehended under the two great circles, which are the representatives of these visible lines. For, since the visible lines appear to coincide with the great circles, the visible angle comprehended under the former must be equal to the visible angle comprehended under the latter. But the visible angle comprehended under the two great circles, when seen from the centre, is of the same magnitude with the spherical angle which they really comprehend, as mathematicians know ; therefore, the visible angle made by any two visible lines is equal to the spherical angle made by the two great circles of the sphere which are their representatives.
5. Hence it is evident, that every visible right-lined triangle will coincide in all its parts with some spherical triangle. The sides of the one will appear equal to the sides of the other, and the angles of the one to the angles of the other, each to each: and, therefore, the whole
of the one triangle will appear equal to the whole of the other. In a word, to the eye they will be one and the same, and have the same mathematical properties. The properties, therefore, of visible right-lined triangles are not the same with the properties of plain triangles, but are the same with those of spherical triangles.
7. Every lesser circle of the sphere will appear a circle to the eye, placed, as we have supposed all along, in the centre of the sphere ; and, on the other hand, every visible circle will appear to coincide with some lesser circle of the sphere.
7. Moreover, the whole surface of the sphere will represent the whole of visible space ; for, since every visible point coincides with some point of the surface of the sphere, and has the same visible place, it follows, that all the parts of the spherical surface taken together, will represent all possible visible places that is, the whole of visible space. And from this it follows, in the last place
8. That every visible figure will be represented by that part of the surface of the sphere on which it might be projected, the eye being in the centre. And every such visible figure will bear the same ratio to the whole of visible space, as the part of the spherical surface which represents it, bears to the whole spherical surface.
The mathematical reader, I hope, will enter into these principles with perfect facility, and will as easily perceive that the following propositions with regard to visible figure and space, which we offer only as a specimen, may be mathematically demonstrated from them, and are not less true nor less evident than the propositions of Euclid, with regard to tangible figures.
Propositions
1. Every right line being produced, will at last return into itself.
2. A right line returning into itself, is the longest possible right line; and all other right lines bear a finite ratio to it.
3. A right line returning into itself, divides the whole of visible space into two equal parts, which will both be comprehended under this right line.
4. The whole of visible space bears a finite ratio to any part of it.
5. Any two right lines being produced, will meet in two points, and mutually bisect each other.
6. If two lines be parallel that is, everywhere equally distant from each other they cannot both be straight.
7. Any right line being given, a point may be found, which is at the same distance from all the points of the given right line.
8. A circle may be parallel to a right line that is, may be equally distant from it in all its parts.
9. Right-lined triangles that are similar, are also equal.
10. Of every right-lined triangle, the three angles taken together, are greater than two right angles.
11. The angles of a right-lined triangle, may all be right angles, or all obtuse angles.
12. Unequal circles are not as the squares of their diameters, nor are their circumferences in the ratio of their diameters.
This small specimen of the geometry of visibles, is intended to lead the reader to a clear and distinct conception of the figure and extension which is presented to the mind by vision; and to demonstrate the truth of what we have affirmed above namely, that those figures
and that extension which are the immediate objects of sight, are not the figures and the extension about which common geometry is employed; that the geometrician, while he looks at his diagram, and demonstrates a proposition, hath a figure presented to his eye, which is only a sign and representative of a tangible figure: that he gives not the least attention to the first, but attends only to the last; and that these two figures have different properties, so that what he demonstrates of the one, is not true of the other.
It deserves, however, to be remarked, that, as a small part of a spherical surface differs not sensibly from a plain surface, so a small part of visible extension differs very little from that extension in length and breadth, which is the object of touch. And it is likewise to be observed, that the human eye is so formed, that an object which is seen distinctly and at one view, can occupy but a small part of visible space; for we never see distinctly what is at a considerable distance from the axis of the eye; and, therefore, when we would see a large object at one view, the eye must be at so great a distance, that the object occupies but a small part of visible space. From these two observations, it follows, that plain figures which are seen at one view, when their planes are not oblique, but direct to the eye, differ little from the visible figures which they present to the eye. The several lines in the tangible figure, have very nearly the same proportion to each other as in the visible; and the angles of the one are very nearly, although not strictly and mathematically, equal to those of the other.
Here are important extracts from the aforementioned book on the Geometry of visibles. This shows why Reids visual geometry can be considered “non-euclidean” as per the currently accepted definitions. The rest of this post are Reid own words.
In this geometry, the definitions of a point of a line, whether straight or curve ; of an angle, whether acute, or right, or obtuse; and of a circle are the same as in common geometry. The mathematical reader will easily enter into the whole mystery of this geometry, if he attends duly to these few evident principles.
1. Supposing the eye placed in the centre of a sphere, every great circle of the sphere will have the same appearance to the eye as if it was a straight line; for the curvature of the circle being turned directly toward the eye, is not perceived by it. And, for the same reason,
any line which is drawn in the plane of a great circle of the sphere, whether it be in reality straight or curve, will appear straight to the eye.
2. Every visible right line will appear to coincide with some great circle of the sphere; and the circumference of that great circle, even when it is produced until it returns into itself, will appear to be a continuation of the same visible right line, all the parts of it being visibly in directum. For the eye, perceiving only the position of objects with regard to itself, and not their distance, will see those points in the same visible place which have the same position with regard to the eye, however different their distances from it may be. Now, since a plane passing through the eye and a given visible right line, will be the plane of some great circle
of the sphere, every point of the visible right line will have the same position as some point of the great circle; therefore, they will both have the same visible place, and coincide to the eye; and the whole circumference of the great circle, continued even until it returns into itself, will appear to be a continuation of the same visible right line.
Hence it follows
3. That every visible right line, when it is continued in directum, as far as it may be continued, will be represented by a great circle of a sphere, in whose centre the eye is placed. It follows
4. That the visible angle comprehended under two visible right lines, is equal to the spherical angle comprehended under the two great circles, which are the representatives of these visible lines. For, since the visible lines appear to coincide with the great circles, the visible angle comprehended under the former must be equal to the visible angle comprehended under the latter. But the visible angle comprehended under the two great circles, when seen from the centre, is of the same magnitude with the spherical angle which they really comprehend, as mathematicians know ; therefore, the visible angle made by any two visible lines is equal to the spherical angle made by the two great circles of the sphere which are their representatives.
5. Hence it is evident, that every visible right-lined triangle will coincide in all its parts with some spherical triangle. The sides of the one will appear equal to the sides of the other, and the angles of the one to the angles of the other, each to each: and, therefore, the whole
of the one triangle will appear equal to the whole of the other. In a word, to the eye they will be one and the same, and have the same mathematical properties. The properties, therefore, of visible right-lined triangles are not the same with the properties of plain triangles, but are the same with those of spherical triangles.
7. Every lesser circle of the sphere will appear a circle to the eye, placed, as we have supposed all along, in the centre of the sphere ; and, on the other hand, every visible circle will appear to coincide with some lesser circle of the sphere.
7. Moreover, the whole surface of the sphere will represent the whole of visible space ; for, since every visible point coincides with some point of the surface of the sphere, and has the same visible place, it follows, that all the parts of the spherical surface taken together, will represent all possible visible places that is, the whole of visible space. And from this it follows, in the last place
8. That every visible figure will be represented by that part of the surface of the sphere on which it might be projected, the eye being in the centre. And every such visible figure will bear the same ratio to the whole of visible space, as the part of the spherical surface which represents it, bears to the whole spherical surface.
The mathematical reader, I hope, will enter into these principles with perfect facility, and will as easily perceive that the following propositions with regard to visible figure and space, which we offer only as a specimen, may be mathematically demonstrated from them, and are not less true nor less evident than the propositions of Euclid, with regard to tangible figures.
Propositions
1. Every right line being produced, will at last return into itself.
2. A right line returning into itself, is the longest possible right line; and all other right lines bear a finite ratio to it.
3. A right line returning into itself, divides the whole of visible space into two equal parts, which will both be comprehended under this right line.
4. The whole of visible space bears a finite ratio to any part of it.
5. Any two right lines being produced, will meet in two points, and mutually bisect each other.
6. If two lines be parallel that is, everywhere equally distant from each other they cannot both be straight.
7. Any right line being given, a point may be found, which is at the same distance from all the points of the given right line.
8. A circle may be parallel to a right line that is, may be equally distant from it in all its parts.
9. Right-lined triangles that are similar, are also equal.
10. Of every right-lined triangle, the three angles taken together, are greater than two right angles.
11. The angles of a right-lined triangle, may all be right angles, or all obtuse angles.
12. Unequal circles are not as the squares of their diameters, nor are their circumferences in the ratio of their diameters.
This small specimen of the geometry of visibles, is intended to lead the reader to a clear and distinct conception of the figure and extension which is presented to the mind by vision; and to demonstrate the truth of what we have affirmed above namely, that those figures
and that extension which are the immediate objects of sight, are not the figures and the extension about which common geometry is employed; that the geometrician, while he looks at his diagram, and demonstrates a proposition, hath a figure presented to his eye, which is only a sign and representative of a tangible figure: that he gives not the least attention to the first, but attends only to the last; and that these two figures have different properties, so that what he demonstrates of the one, is not true of the other.
It deserves, however, to be remarked, that, as a small part of a spherical surface differs not sensibly from a plain surface, so a small part of visible extension differs very little from that extension in length and breadth, which is the object of touch. And it is likewise to be observed, that the human eye is so formed, that an object which is seen distinctly and at one view, can occupy but a small part of visible space; for we never see distinctly what is at a considerable distance from the axis of the eye; and, therefore, when we would see a large object at one view, the eye must be at so great a distance, that the object occupies but a small part of visible space. From these two observations, it follows, that plain figures which are seen at one view, when their planes are not oblique, but direct to the eye, differ little from the visible figures which they present to the eye. The several lines in the tangible figure, have very nearly the same proportion to each other as in the visible; and the angles of the one are very nearly, although not strictly and mathematically, equal to those of the other.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Enter the Idomenians (Beings with only one Eye)
Reid asks us to imagine beings called Idomenians as a way for us to better understand his arguments. He does this by introducing a traveller and telling us his narrative. Whether this person is real or not is difficult to say. Maybe Reid was alluding to some people who knew more ?
The rest of this post are all Reids own words
Although, therefore, we have found many instances of natural signs which have no similitude to the things signified, this is not the case with regard to visible figure. It hath, in all cases, such a similitude to the thing signified by it, as a plan or profile hath to that which it represents; and, in some cases, the sign and thing signified have to all sense the same figure and the same proportions. If we could find a being endued with sight only, without any other external sense, and capable of reflecting and reasoning upon what he sees, the notions and philosophical speculations of such a being, might assist us in the difficult task of distinguishing the perceptions which we have purely by sight, from those which derive their origin from other senses. Let us suppose such a being, and conceive, as well as we can, what notion he would have of visible objects, and what conclusions he would deduce from them. We must not conceive him disposed by his constitution, as we are, to consider the visible appearance as a sign of something else: it is no sign to him, because there is nothing signified by it; and, therefore, we must suppose him as much disposed to attend to the visible figure and extension of bodies, as we are disposed to attend to their tangible figure and extension.
If various figures were presented to his sense, he might, without doubt, as they grow familiar, compare them together, and perceive wherein they agree, and wherein they differ. He might perceive visible objects to have length and breadth, but could have no notion of a third dimension, any more than we can have of a fourth. All visible objects would appear to be terminated by lines, straight or curve; and objects terminated by the same visible lines, would occupy the same place, and fill the same part of visible space. It would not be possible for him to conceive one object to be behind another, or one to be nearer, another more distant.
To us, who conceive three dimensions, a line may be conceived straight; or it may be conceived incurvated in one dimension, and straight in another; or, lastly, it may be incurvated in two dimensions. Suppose a line to be drawn upwards and downwards, its length makes one dimension, which we shall call upwards and downwards; and there are two dimensions remaining, according to which it may be straight or curve. It may be bent to the right or to the left, and, if it has no bending either to right or left, it is straight in this dimension. But supposing it straight in this dimension of right and left, there is still another dimension remaining, in which it may be curve; for it may be bent backwards or forwards.
When we conceive a tangible straight line, we exclude curvature in either of these two dimensions: and as what is conceived to be excluded, must be conceived, as well as what is conceived to be included, it follows that all the three dimensions enter into our conception of a straight line. Its length is one dimension, its straightness in two other dimensions is included, or curvature in these two dimensions excluded, in the conception of it.
The being we have supposed, having no conception of more than two dimensions, of which the length of a line is one, cannot possibly conceive it either straight or curve in more than one dimension; so that, in his conception of a right line, curvature to the right hand or left is excluded; but curvature backwards or forwards cannot be excluded, because he neither hath, nor can have any conception of such curvature. Hence we see the reason that a line which is straight to the eye, may return into itself; for its being straight to the eye, implies only straightness in one dimension; and a line which is straight in one dimension may, notwithstanding, be curved in another dimension, and so may return into itself.
To us, who conceive three dimensions, a surface is that which hath length and breadth, excluding thickness; and a surface may be either plain in this third dimension, or it may be incurvated: so that the notion of a third dimension enters into our conception of a surface; for it is only by means of this third dimension that we can distinguish surfaces into plain and curve surfaces; and neither one nor the other can be conceived without conceiving a third dimension.
The being we have supposed, having no conception of a third dimension, his visible figures have length and breadth indeed; but thickness is neither included nor excluded, being a thing of which he has no conception. And, therefore, visible figures, although they have length and breadth, as surfaces have, yet they are neither plain surfaces nor curve surfaces. For a curve surface implies curvature in a third dimension, and a plain surface implies the want of curvature in a third dimension; and such a being can conceive neither of these, because he has no conception of a third dimension. Moreover, although he hath a distinct conception of the inclination of two lines which make an angle, yet he can neither conceive a plain angle nor a spherical angle. Even his notion of a point is somewhat less determined than ours. In the notion of a point, we exclude length, breadth, and thickness; he excludes length and breadth, but cannot either exclude, or include thickness, because he hath no conception of it.
Having thus settled the notions which such a being as we have supposed might form of mathematical points, lines, angles, and figures, it is easy to see, that, by comparing these together, and reasoning about them, he might discover their relations, and form geometrical conclusions built upon self-evident principles. He might likewise, without doubt, have the same notions of numbers as we have, and form a system of arithmetic.
It is not material to say in what order he might proceed in such discoveries, or how much time and pains he might employ about them, but what such a being, by reason and ingenuity, without any materials of sensation but those of sight only, might discover.
As it is more difficult to attend to a detail of possibilities than of facts, even of slender authority, I shall beg leave to give an extract from the travels of Johannes Rudolphus Anepigraphus, a Rosicrucian philosopher, who having, by deep study of the occult sciences, acquired the art of transporting himself to various sublunary regions, and of conversing with various orders of intelligences, in the course of his adventures became acquainted with an order of beings exactly such as I have supposed.
How they communicate their sentiments to one another, and by what means he became acquainted with their language, and was initiated into their philosophy; as well as of many other particulars, which might have gratified the curiosity of his readers, and, perhaps, added credibility to his relation, he hath not thought fit to inform us; these being matters proper for adepts only to know.
His account of their philosophy is as follows:
The Idomenians, " saith he, " are many of them very ingenious, and much given to contemplation. In arithmetic, geometry, metaphysics, and physics, they have most elaborate systems. In the two latter, indeed, they have had many disputes carried on with great subtilty, and are divided into various sects; yet in the two former there hath been no less unanimity than among the human species. Their principles relating to numbers and arithmetic, making allowance for their notation, differ in nothing from ours but their geometry differs very considerably."
As our author's account of the geometry of the Idomenians agrees in everything with the geometry of visibles, of which we have already given a specimen, we shall pass over it. He goes on thus: "Colour, extension, and figure, are conceived to be the essential properties of body. A very considerable sect maintains, that colour is the essence of body. If there had been no colour, say they, there had been no perception or sensation. Colour is all that we perceive, or can conceive, that is peculiar to body; extension and figure being modes common to body and to empty space. And if we should suppose a body to be annihilated, colour is the only thing in it that can be annihilated; for its place, and consequently the figure and extension of that place, must remain, and cannot be imagined not to exist. These philosophers hold space to be the place of all bodies, immovable and indestructible, without figure and similar in all its parts, incapable of increase or diminution, yet not unmeasurable; for every least part of space bears a finite ratio to the whole. So that with them the whole extent of space is the common and natural measure of everything that hath length and breadth; and the magnitude of every body and of every figure is expressed by its being such a part of the universe. In like manner, the common and natural measure of length is an infinite right line, which, as hath been before observed, returns into itself, and hath no limits, but bears a finite ratio to every other line.
"As to their natural philosophy, it is now acknowledged by the wisest of them to have been for many ages in a very low state. The philosophers observing, that body can differ from another only in colour, figure, or magnitude, it was taken for granted, that all their particular qualities must arise from the various combinations of these their essential attributes; and, therefore, it was looked upon as the end of natural philosophy, to shew how the various combinations of these three qualities in different bodies produced all the phaenomena of nature. It would be endless to enumerate the various systems that were invented with this view, and the disputes that were carried on for ages; the followers of every system exposing the weak sides of other systems, and palliating those of their own with great art.
At last, some free and facetious spirits, wearied with eternal disputation, and the labour of patching and propping weak systems, began to complain of the subtilty of nature; of the infinite changes that bodies undergo in figure, colour, and magnitude; and of the difficulty of accounting for these appearances making this a pretence for giving up all inquiries into the causes of things, as vain and fruitless.
These wits had ample matter of mirth and ridicule in the systems of philosophers; and, finding it an easier task to pull down than to build or support, and that every sect furnished them with arms and auxiliaries to destroy another, they began to spread mightily, and went on with great success. Thus philosophy gave way to scepticism and irony, and those systems which had been the work of ages, and the admiration of the learned, became the jest of the vulgar: for even the vulgar readily took part in the triumph over a kind of learning which they had long suspected, because it produced nothing but wrangling and altercation. The wits, having now acquired great reputation, and being flushed with success, began to think their triumph incomplete, until every pretence to knowledge was overturned ; and accordingly began their attacks upon arithmetic, geometry, and even upon the common notions of untaught Idomenians. So difficult it hath always been," says our author, "for great conquerors to know where to stop.
In the meantime, natural philosophy began to rise from its ashes, under the direction of a person of great genius, who is looked upon as having had something in him above Idomenian nature. He observed, that the Idomenian faculties were certainly intended for contemplation, and that the works of nature were a nobler subject to exercise them upon, than the follies of systems, or the errors of the learned; and being sensible of the difficulty of finding out the causes of natural things, he proposed, by accurate observation of the phaenomena of nature, to find out the rules according to which they happen, without inquiring into the causes of those rules. In this he made considerable progress himself, and planned out much work for his followers, who call themselves inductive philosophers. The sceptics look with envy upon this rising sect, as eclipsing their reputation, and threatening to limit their empire; but they are at a loss on what hand to attack it. The vulgar begin to reverence it as producing useful discoveries.
"It is to be observed, that every Idomenian firmly believes, that two or more bodies may exist in the same place. For this they have the testimony of sense, and they can no more doubt of it, than they can doubt whether they have any perception at all. They often see two bodies meet and coincide in the same place, and separate again, without having undergone any change in their sensible qualities by this penetration. When two bodies meet, and occupy the same place, commonly one only appears in that place, and the other disappears.
That which continues to appear is said to overcome, the other to be overcome." To this quality of bodies they gave a name, which our author tells us hath no word answering to it in any human language. And, therefore, after making a long apology, which I omit, he begs leave to call it the over-coming quality of bodies. He assures us, that " the speculations which had been raised about this single quality of bodies, and the hypotheses contrived to account for it, were sufficient to fill many volumes. Nor have there been fewer hypotheses invented by their philosophers, to account for the changes of magnitude and figure; which, in most bodies that move, they perceive to be in a continual fluctuation. The founder of the inductive sect, believing it to be above the reach of Idomenian faculties, to discover the real causes of these phenomena, applied himself to find from observation, by what laws they are connected together; and discovered many mathematical ratios and relations concerning the motions, magnitudes, figures, and overcoming quality of bodies, which constant experience confirms. But the opposers of this sect choose rather to content themselves with feigned causes of these phaenomena, than to acknowledge the real laws whereby they are governed, which humble their pride, by being confessedly unaccountable. '
Thus far Johannes Rudolphus Anepigraphus. Whether this Anepigraphus be the same who is recorded among the Greek alchemistical writers not yet published, by Borrichius, Fabricius, and others, I do not pretend to determine. The identity of their name, and the similitude of their studies, although no slight arguments, yet are not absolutely conclusive. Nor will I take upon me to judge of the narrative of this learned traveller, by the external marks of his credibility; I shall confine myself to those which the critics call internal. It would even be of small importance to inquire, whether the Idomenians have a real, or only an ideal existence; since this is disputed among the learned with regard to things with which we are more nearly connected. The important question is, whether the account above given, is a just account of their geometry and philosophy? We have all the faculties which they have, with the addition of others which they have not; we may, therefore, form some judgment of their philosophy and geometry, by separating from all others, the perceptions we have by sight and reasoning upon them. As far as I am able to judge in this way, after a careful examination, their geometry must be such as Anepigraphus hath described. Nor does his account of their philosophy appear to contain any evident marks of imposture; although here, no doubt, proper allowance is to be made for liberties which travellers take, as well as for involuntary mistakes which they are apt to fall into.
Reid asks us to imagine beings called Idomenians as a way for us to better understand his arguments. He does this by introducing a traveller and telling us his narrative. Whether this person is real or not is difficult to say. Maybe Reid was alluding to some people who knew more ?
The rest of this post are all Reids own words
Although, therefore, we have found many instances of natural signs which have no similitude to the things signified, this is not the case with regard to visible figure. It hath, in all cases, such a similitude to the thing signified by it, as a plan or profile hath to that which it represents; and, in some cases, the sign and thing signified have to all sense the same figure and the same proportions. If we could find a being endued with sight only, without any other external sense, and capable of reflecting and reasoning upon what he sees, the notions and philosophical speculations of such a being, might assist us in the difficult task of distinguishing the perceptions which we have purely by sight, from those which derive their origin from other senses. Let us suppose such a being, and conceive, as well as we can, what notion he would have of visible objects, and what conclusions he would deduce from them. We must not conceive him disposed by his constitution, as we are, to consider the visible appearance as a sign of something else: it is no sign to him, because there is nothing signified by it; and, therefore, we must suppose him as much disposed to attend to the visible figure and extension of bodies, as we are disposed to attend to their tangible figure and extension.
If various figures were presented to his sense, he might, without doubt, as they grow familiar, compare them together, and perceive wherein they agree, and wherein they differ. He might perceive visible objects to have length and breadth, but could have no notion of a third dimension, any more than we can have of a fourth. All visible objects would appear to be terminated by lines, straight or curve; and objects terminated by the same visible lines, would occupy the same place, and fill the same part of visible space. It would not be possible for him to conceive one object to be behind another, or one to be nearer, another more distant.
To us, who conceive three dimensions, a line may be conceived straight; or it may be conceived incurvated in one dimension, and straight in another; or, lastly, it may be incurvated in two dimensions. Suppose a line to be drawn upwards and downwards, its length makes one dimension, which we shall call upwards and downwards; and there are two dimensions remaining, according to which it may be straight or curve. It may be bent to the right or to the left, and, if it has no bending either to right or left, it is straight in this dimension. But supposing it straight in this dimension of right and left, there is still another dimension remaining, in which it may be curve; for it may be bent backwards or forwards.
When we conceive a tangible straight line, we exclude curvature in either of these two dimensions: and as what is conceived to be excluded, must be conceived, as well as what is conceived to be included, it follows that all the three dimensions enter into our conception of a straight line. Its length is one dimension, its straightness in two other dimensions is included, or curvature in these two dimensions excluded, in the conception of it.
The being we have supposed, having no conception of more than two dimensions, of which the length of a line is one, cannot possibly conceive it either straight or curve in more than one dimension; so that, in his conception of a right line, curvature to the right hand or left is excluded; but curvature backwards or forwards cannot be excluded, because he neither hath, nor can have any conception of such curvature. Hence we see the reason that a line which is straight to the eye, may return into itself; for its being straight to the eye, implies only straightness in one dimension; and a line which is straight in one dimension may, notwithstanding, be curved in another dimension, and so may return into itself.
To us, who conceive three dimensions, a surface is that which hath length and breadth, excluding thickness; and a surface may be either plain in this third dimension, or it may be incurvated: so that the notion of a third dimension enters into our conception of a surface; for it is only by means of this third dimension that we can distinguish surfaces into plain and curve surfaces; and neither one nor the other can be conceived without conceiving a third dimension.
The being we have supposed, having no conception of a third dimension, his visible figures have length and breadth indeed; but thickness is neither included nor excluded, being a thing of which he has no conception. And, therefore, visible figures, although they have length and breadth, as surfaces have, yet they are neither plain surfaces nor curve surfaces. For a curve surface implies curvature in a third dimension, and a plain surface implies the want of curvature in a third dimension; and such a being can conceive neither of these, because he has no conception of a third dimension. Moreover, although he hath a distinct conception of the inclination of two lines which make an angle, yet he can neither conceive a plain angle nor a spherical angle. Even his notion of a point is somewhat less determined than ours. In the notion of a point, we exclude length, breadth, and thickness; he excludes length and breadth, but cannot either exclude, or include thickness, because he hath no conception of it.
Having thus settled the notions which such a being as we have supposed might form of mathematical points, lines, angles, and figures, it is easy to see, that, by comparing these together, and reasoning about them, he might discover their relations, and form geometrical conclusions built upon self-evident principles. He might likewise, without doubt, have the same notions of numbers as we have, and form a system of arithmetic.
It is not material to say in what order he might proceed in such discoveries, or how much time and pains he might employ about them, but what such a being, by reason and ingenuity, without any materials of sensation but those of sight only, might discover.
As it is more difficult to attend to a detail of possibilities than of facts, even of slender authority, I shall beg leave to give an extract from the travels of Johannes Rudolphus Anepigraphus, a Rosicrucian philosopher, who having, by deep study of the occult sciences, acquired the art of transporting himself to various sublunary regions, and of conversing with various orders of intelligences, in the course of his adventures became acquainted with an order of beings exactly such as I have supposed.
How they communicate their sentiments to one another, and by what means he became acquainted with their language, and was initiated into their philosophy; as well as of many other particulars, which might have gratified the curiosity of his readers, and, perhaps, added credibility to his relation, he hath not thought fit to inform us; these being matters proper for adepts only to know.
His account of their philosophy is as follows:
The Idomenians, " saith he, " are many of them very ingenious, and much given to contemplation. In arithmetic, geometry, metaphysics, and physics, they have most elaborate systems. In the two latter, indeed, they have had many disputes carried on with great subtilty, and are divided into various sects; yet in the two former there hath been no less unanimity than among the human species. Their principles relating to numbers and arithmetic, making allowance for their notation, differ in nothing from ours but their geometry differs very considerably."
As our author's account of the geometry of the Idomenians agrees in everything with the geometry of visibles, of which we have already given a specimen, we shall pass over it. He goes on thus: "Colour, extension, and figure, are conceived to be the essential properties of body. A very considerable sect maintains, that colour is the essence of body. If there had been no colour, say they, there had been no perception or sensation. Colour is all that we perceive, or can conceive, that is peculiar to body; extension and figure being modes common to body and to empty space. And if we should suppose a body to be annihilated, colour is the only thing in it that can be annihilated; for its place, and consequently the figure and extension of that place, must remain, and cannot be imagined not to exist. These philosophers hold space to be the place of all bodies, immovable and indestructible, without figure and similar in all its parts, incapable of increase or diminution, yet not unmeasurable; for every least part of space bears a finite ratio to the whole. So that with them the whole extent of space is the common and natural measure of everything that hath length and breadth; and the magnitude of every body and of every figure is expressed by its being such a part of the universe. In like manner, the common and natural measure of length is an infinite right line, which, as hath been before observed, returns into itself, and hath no limits, but bears a finite ratio to every other line.
"As to their natural philosophy, it is now acknowledged by the wisest of them to have been for many ages in a very low state. The philosophers observing, that body can differ from another only in colour, figure, or magnitude, it was taken for granted, that all their particular qualities must arise from the various combinations of these their essential attributes; and, therefore, it was looked upon as the end of natural philosophy, to shew how the various combinations of these three qualities in different bodies produced all the phaenomena of nature. It would be endless to enumerate the various systems that were invented with this view, and the disputes that were carried on for ages; the followers of every system exposing the weak sides of other systems, and palliating those of their own with great art.
At last, some free and facetious spirits, wearied with eternal disputation, and the labour of patching and propping weak systems, began to complain of the subtilty of nature; of the infinite changes that bodies undergo in figure, colour, and magnitude; and of the difficulty of accounting for these appearances making this a pretence for giving up all inquiries into the causes of things, as vain and fruitless.
These wits had ample matter of mirth and ridicule in the systems of philosophers; and, finding it an easier task to pull down than to build or support, and that every sect furnished them with arms and auxiliaries to destroy another, they began to spread mightily, and went on with great success. Thus philosophy gave way to scepticism and irony, and those systems which had been the work of ages, and the admiration of the learned, became the jest of the vulgar: for even the vulgar readily took part in the triumph over a kind of learning which they had long suspected, because it produced nothing but wrangling and altercation. The wits, having now acquired great reputation, and being flushed with success, began to think their triumph incomplete, until every pretence to knowledge was overturned ; and accordingly began their attacks upon arithmetic, geometry, and even upon the common notions of untaught Idomenians. So difficult it hath always been," says our author, "for great conquerors to know where to stop.
In the meantime, natural philosophy began to rise from its ashes, under the direction of a person of great genius, who is looked upon as having had something in him above Idomenian nature. He observed, that the Idomenian faculties were certainly intended for contemplation, and that the works of nature were a nobler subject to exercise them upon, than the follies of systems, or the errors of the learned; and being sensible of the difficulty of finding out the causes of natural things, he proposed, by accurate observation of the phaenomena of nature, to find out the rules according to which they happen, without inquiring into the causes of those rules. In this he made considerable progress himself, and planned out much work for his followers, who call themselves inductive philosophers. The sceptics look with envy upon this rising sect, as eclipsing their reputation, and threatening to limit their empire; but they are at a loss on what hand to attack it. The vulgar begin to reverence it as producing useful discoveries.
"It is to be observed, that every Idomenian firmly believes, that two or more bodies may exist in the same place. For this they have the testimony of sense, and they can no more doubt of it, than they can doubt whether they have any perception at all. They often see two bodies meet and coincide in the same place, and separate again, without having undergone any change in their sensible qualities by this penetration. When two bodies meet, and occupy the same place, commonly one only appears in that place, and the other disappears.
That which continues to appear is said to overcome, the other to be overcome." To this quality of bodies they gave a name, which our author tells us hath no word answering to it in any human language. And, therefore, after making a long apology, which I omit, he begs leave to call it the over-coming quality of bodies. He assures us, that " the speculations which had been raised about this single quality of bodies, and the hypotheses contrived to account for it, were sufficient to fill many volumes. Nor have there been fewer hypotheses invented by their philosophers, to account for the changes of magnitude and figure; which, in most bodies that move, they perceive to be in a continual fluctuation. The founder of the inductive sect, believing it to be above the reach of Idomenian faculties, to discover the real causes of these phenomena, applied himself to find from observation, by what laws they are connected together; and discovered many mathematical ratios and relations concerning the motions, magnitudes, figures, and overcoming quality of bodies, which constant experience confirms. But the opposers of this sect choose rather to content themselves with feigned causes of these phaenomena, than to acknowledge the real laws whereby they are governed, which humble their pride, by being confessedly unaccountable. '
Thus far Johannes Rudolphus Anepigraphus. Whether this Anepigraphus be the same who is recorded among the Greek alchemistical writers not yet published, by Borrichius, Fabricius, and others, I do not pretend to determine. The identity of their name, and the similitude of their studies, although no slight arguments, yet are not absolutely conclusive. Nor will I take upon me to judge of the narrative of this learned traveller, by the external marks of his credibility; I shall confine myself to those which the critics call internal. It would even be of small importance to inquire, whether the Idomenians have a real, or only an ideal existence; since this is disputed among the learned with regard to things with which we are more nearly connected. The important question is, whether the account above given, is a just account of their geometry and philosophy? We have all the faculties which they have, with the addition of others which they have not; we may, therefore, form some judgment of their philosophy and geometry, by separating from all others, the perceptions we have by sight and reasoning upon them. As far as I am able to judge in this way, after a careful examination, their geometry must be such as Anepigraphus hath described. Nor does his account of their philosophy appear to contain any evident marks of imposture; although here, no doubt, proper allowance is to be made for liberties which travellers take, as well as for involuntary mistakes which they are apt to fall into.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Initial Comments on the Geometry of Visibles
Let’s have a closer look at what is being said by Reid. I am consolidating some of the late R.B. Angells analysis with some of my own humble interpretations. R.B. Angell dubs the Geometry of Visibles as GoV and we are comparing Euclidean Geometry to GoV.
This should help show the difference between Euclidean geometry and the non-Euclidean GOV.
1. Euclidean: A straight line cannot be a circle
GoV: A straight line can be a circle.
i.e. a visual straight line can be a closed line with all points on it equidistant from a polar point in the visual field. Consider the horizon, with a point directly overhead its center.
VP: Like viewing from inside a Hula Hoop. You can turn 360 degrees, the horizon always looks straight, but you have turned a full circle.
2. Euclidean: Every straight line or plane is infinitely extendable
GoV: No straight line is infinitely extendable.
If we extend any straight line segment in the visible field it eventually returns on itself. It is thus finite, though unbounded. Again consider the horizon.
VP: By turning 360 you are back to where you started. The horizon is not infinite, in fact as we saw earlier infinity is a logical fallacy.
3. Euclidean: Two straight lines intersect at most in one point.
GoV: Every pair of straight lines intersects at two points.
Imagine standing in the middle of a straight railroad track. The visual lines associated with the two rails are demonstrably visually straight in every segment. They “appear” perfectly straight, not curved visually. Yet these visually straight lines meet at two points which are opposite each other on the horizon, and they enclose a substantial region on the visual field
VP: Looking down the railway tracks we see the lines converging and intersecting at a distant point. By turning 180 and again looking down the track you again see them meeting at another point. Two straight lines intersecting at two points.
4. Euclidean: Two straight lines, cut by a third straight line perpendicular to both never intersect
GoV: Two straight lines, cut by a third straight line perpendicular to both always intersect.
The two rails both appearing visually straight, are cut by the straight edge of the railroad tie at our feet, and this tie is perpendicular visually to both of them; yet the two visual rays intersect twice.
VP: Parallel lines converge and visually intersect twice, even though we know the railroad tracks remain equally spaced throughout and never intersect.
5. Euclidean: All equilateral triangles have the same interior angles
GoV: All equilateral triangles do not have the same interior angles
Consider a large visual triangle, like that between a star due East on the horizon, a star due North on the horizon and a star directly overhead. In this case equal visual straight lines connect the three stars, so the triangle is equilateral. Yet the angles are all right angles and thus are larger than angles of equilateral triangles which are 60 degrees.
VP: This is analogous to the concept of spherical triangles, where the angles are greater (and can be right angled). Consider the “globe argument” of an ant making 3 right turns on a sphere and getting back to the starting point on the triangle.
6. Euclidean: The sum of the interior angles of a triangle equals two right angles
GoV: The sum of the interior angles of a triangle is always greater than two right angles.
See the Visual triangle above. This would be found to be the case with all other visual triangles given careful measurement.
VP: Gauss famously measured the angles of the mountains Brocken, Hohenhagen and Inselberg (BHI). There is close agreement between the measurements of this triangle and the predictions of Euclidean geometry, only when the mountain tops are treated as three points on a sphere.
7. Euclidean: The four angles of a rectangle are all right angles
GoV: The four angles of a rectangle are always larger than right angles.
This is clear if we measure the visual angles of a picture frame. We can approach a picture frame so that the sides are not only all straight, but the angles are all visually equal. Yet the angles are all visually obtuse
VP: When walking towards a door, notice that the angles of the door frame can be seen as stated above. When passing through the door, the corners of the frame will appear to get bigger than 90 degrees and approach 180 as you pass through.
Another example of this is when you look at the corners of your room, one at a time. Each corner has visual angles shaped like a flattened out Y and the angles are all visually larger than 90 degrees, even though we know the house-builders made sure the walls are all at 90 degrees to the ceilings and to each other.
Note that you can draw each corner separately on a piece of paper, but you could never draw all four corners at once in the same drawing, because the paper is a Euclidean Object.
However, this does not mean we cannot see non-Euclidean quadrilaterals. It is not possible to represent the room how it appears to us on paper. If we thought we could draw it, we would be guilty in Reids words of failing to see that the “visible figure presented to the eye, is only the representative of the tangible figure upon which our attention is fixed and what we demonstrate to be true of the one, is not true of the other”.
Let’s have a closer look at what is being said by Reid. I am consolidating some of the late R.B. Angells analysis with some of my own humble interpretations. R.B. Angell dubs the Geometry of Visibles as GoV and we are comparing Euclidean Geometry to GoV.
This should help show the difference between Euclidean geometry and the non-Euclidean GOV.
1. Euclidean: A straight line cannot be a circle
GoV: A straight line can be a circle.
i.e. a visual straight line can be a closed line with all points on it equidistant from a polar point in the visual field. Consider the horizon, with a point directly overhead its center.
VP: Like viewing from inside a Hula Hoop. You can turn 360 degrees, the horizon always looks straight, but you have turned a full circle.
2. Euclidean: Every straight line or plane is infinitely extendable
GoV: No straight line is infinitely extendable.
If we extend any straight line segment in the visible field it eventually returns on itself. It is thus finite, though unbounded. Again consider the horizon.
VP: By turning 360 you are back to where you started. The horizon is not infinite, in fact as we saw earlier infinity is a logical fallacy.
3. Euclidean: Two straight lines intersect at most in one point.
GoV: Every pair of straight lines intersects at two points.
Imagine standing in the middle of a straight railroad track. The visual lines associated with the two rails are demonstrably visually straight in every segment. They “appear” perfectly straight, not curved visually. Yet these visually straight lines meet at two points which are opposite each other on the horizon, and they enclose a substantial region on the visual field
VP: Looking down the railway tracks we see the lines converging and intersecting at a distant point. By turning 180 and again looking down the track you again see them meeting at another point. Two straight lines intersecting at two points.
4. Euclidean: Two straight lines, cut by a third straight line perpendicular to both never intersect
GoV: Two straight lines, cut by a third straight line perpendicular to both always intersect.
The two rails both appearing visually straight, are cut by the straight edge of the railroad tie at our feet, and this tie is perpendicular visually to both of them; yet the two visual rays intersect twice.
VP: Parallel lines converge and visually intersect twice, even though we know the railroad tracks remain equally spaced throughout and never intersect.
5. Euclidean: All equilateral triangles have the same interior angles
GoV: All equilateral triangles do not have the same interior angles
Consider a large visual triangle, like that between a star due East on the horizon, a star due North on the horizon and a star directly overhead. In this case equal visual straight lines connect the three stars, so the triangle is equilateral. Yet the angles are all right angles and thus are larger than angles of equilateral triangles which are 60 degrees.
VP: This is analogous to the concept of spherical triangles, where the angles are greater (and can be right angled). Consider the “globe argument” of an ant making 3 right turns on a sphere and getting back to the starting point on the triangle.
6. Euclidean: The sum of the interior angles of a triangle equals two right angles
GoV: The sum of the interior angles of a triangle is always greater than two right angles.
See the Visual triangle above. This would be found to be the case with all other visual triangles given careful measurement.
VP: Gauss famously measured the angles of the mountains Brocken, Hohenhagen and Inselberg (BHI). There is close agreement between the measurements of this triangle and the predictions of Euclidean geometry, only when the mountain tops are treated as three points on a sphere.
7. Euclidean: The four angles of a rectangle are all right angles
GoV: The four angles of a rectangle are always larger than right angles.
This is clear if we measure the visual angles of a picture frame. We can approach a picture frame so that the sides are not only all straight, but the angles are all visually equal. Yet the angles are all visually obtuse
VP: When walking towards a door, notice that the angles of the door frame can be seen as stated above. When passing through the door, the corners of the frame will appear to get bigger than 90 degrees and approach 180 as you pass through.
Another example of this is when you look at the corners of your room, one at a time. Each corner has visual angles shaped like a flattened out Y and the angles are all visually larger than 90 degrees, even though we know the house-builders made sure the walls are all at 90 degrees to the ceilings and to each other.
Note that you can draw each corner separately on a piece of paper, but you could never draw all four corners at once in the same drawing, because the paper is a Euclidean Object.
However, this does not mean we cannot see non-Euclidean quadrilaterals. It is not possible to represent the room how it appears to us on paper. If we thought we could draw it, we would be guilty in Reids words of failing to see that the “visible figure presented to the eye, is only the representative of the tangible figure upon which our attention is fixed and what we demonstrate to be true of the one, is not true of the other”.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Great post VP, I spent most of my evening reading Thomas Reid's work, a long with some videos from Wildberger - look forward to working my way through the rest of your posts!

csp- Posts : 424
Points : 4726
Reputation : 1054
Join date : 2016-01-04
Location : Australia
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
vortexpuppy wrote: If you like, the non-Euclidean geometry of an Eye’s direct vision capabilities, has been “removed from the Eye”, and replaced by Euclidean concepts. We are then led to believe that the Eye sees in picture representations on a plane, and that the retina is like a plane surface. If you like, the “curve” of the eye has been placed outside the Eye and we are then told that this is the spherical ball world we live on.
Brilliant VP, makes complete Sense
Hey Gang, Google "all seeing eye" Images just to remind yourself again of the deception.
I found myself just shaking my head.
Last edited by vortexkitten on Sat Jul 02, 2016 4:46 pm; edited 1 time in total
vortexkitten- Posts : 37
Points : 3375
Reputation : 87
Join date : 2015-12-31
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Some comments and questions on Light and Visibles
Light is said to be electromagnetic radiation within a certain range of the electromagnetic spectrum. This is called Visible Light, the main source of which is the Sun. Visible light means that the light is visible to the human Eye.
Light is said to be the medium, by which Vision is transported to the Eye. It is said to be both a particle (material) and a wave (immaterial) depending on circumstance and Observation. Light is generally accepted to emanate from all parts of a Luminary (or reflected from an Object that is illuminated) and propagate in all directions in straight lines, as so called Visual Rays that enter the Eye.
Now without Light we have no Vision, since no Object can be seen without Light. Shut your eyes to prove this to yourself. Sight or visual perception then, is the ability to interpret the environment by processing information that is apparently “somehow contained” in visible light.
The interplay between Light and Matter continuously creates visibles, waiting to be seen by the correctly situated optical instrument, such as the Eye. The visibles (figure, extension, color, etc.) keep changing, they neither stop nor start, change is all there is.
Light and visibles seems to live in a different geometric space to our Euclidean world of solid objects. It is a seemingly paradoxical space that co-exists with our tangible world. A kind of dual role is played. It is part of our world, but somehow not a part of it either. It takes up no volume in our local reality and extends in every direction, overlapping and intersecting. In this space two visibles can be in the same place at the same time (e.g. two colors mixing), in direct contrast to a Euclidean space where no two bodies or particles can occupy the same space.
Now, I know that the Objects are still there when I shut my eyes and I bump into them in the dark, so my Euclidean world doesn’t go away when there is no light, only the visual space is gone.
Similarly, I know that visibles exist whether I see them or not. They are created by objects, their environment and illumination, by the colors, the light and shade, etc. and are unique to a particular viewpoint or eye position. They are continuously available for anyone who wants to look. Just as a falling tree will most definitely make a sound in a forest, even when nobody is there to hear it, so will a visible exist, whether somebody is looking or not.
Visibles are a common sense data that we can all share. “Come over here and have look at this”, you say to your friends, when you want to share your view of an object of interest. We have all stopped at viewing places during our travels, to marvel at some spectacular scenery. Whether somebody is looking or not, this visible at this particular viewpoint is a unique, real entity and is independent of the mind. So it seems that:
Visibles are entities of a 2 -Dimensional geometrical space, seen by an optical instrument such as the Eye, of Objects in 3D Euclidean space that are illuminated.
Do individual visibles belong to a set of all possible views, seen from all possible angles, and from all possible Eyes? The visibles change all the time, as the Earth and its animate and inanimate matter “lives and dies” and as we move around and the light changes, etc. Is this set of all possible visibles then finite?
We can never individually experience even a fraction of all the possible visibles, only collectively maybe? Just as we view visibles, so do all other animals, insects and creatures have their view of parts of the total visible space. The plant world (e.g. sunflowers) likewise strive to see the light with their own “eyes” and experience the amazing Light-Matter spectacle of Nature.
Does Light create its own 2D visual geometric space as it propagates? Does it create the visibles in this space as it illuminates? What role does the matter play? Simply that of a reflecting surface? A surface of a physical Object with individual material properties, where reflection is dependent only on the composition of the top few atom layers?
According to modern science, light propagates in straight lines, filling a spherical voulme, with a very fast but finite speed. My experience of light is local and instantaneous. It is obviously a local phenomenon that comes and goes with day and night.
Thought: If a filter could be put directly in front of the Sun that stopped all illumination, and then suddenly pulled away, then I am sure that it would not be dark for 8 minutes until the light reached us ;-) Pity we can’t do that experiment (yet).
It is preposterous to think that Sunlight could come from so far away. Light is said to propagate in all directions as a point source filling a spherical volume as it expands on its way to us. The distance it would expand in reaching us, is the same as the radius of the Earths alleged Orbit round the sun. The Sun to Earth distance is considered to be 109 times the Suns diameter or 218 times its radius. You can fit 218 Suns in the distance between Earth and the Sun. This means that each side of a 1 cm square surface of the Sun, will be 218 cm when it reaches the Earth. So the area is multiplied 218 * 218 times = 47.524 cm squared. The altitude of the visual ray pyramid is the distance from the Earth to the Sun. So the volume of the quadrangular light pyramid (apex at Sun, base on Earth) is 47.524 * 15.000.000.000.000 cm = 712.860.000.000.000.000 cm cubed, and that is only from 1 cm of surface?
What happens to the light? It goes on forever? Never dissipating? What happens to the light when it reaches our eye? Where does it all go? If Light is considered particulate (photon), how the hell can an eye contain and absorb all these particle light rays? What capacity must the eye then have, considering the volume of light reaching it? Hmm..., there is still much said about Light that makes no sense yet.
The geometric space of visibles can be tentatively visualized as a sort of surface, but not one that is part of any 3D Object. I try not to think of artificial Cartesian coordinates and XYZ Axes. It is arranged more in the 2 Dimensions of the natural (cardinal) directions of up/down, left/right.
We do experience an eye shaped spheroidal visual space around us, but this geometrical space should not be directly equated with Spherical Geometry (not even oblate spheroid geometry ;-). It is a useful analog, with many geometrical truths common to both, otherwise ancient navigation and astronomy would not have worked within the error limits that it does, but they are not exactly the same.
The basic axioms of the GOV model, are that of a bi-polar (double) elliptic geometry, the modern name for “spherical geometry”. Bi-polar means that anti-podal (opposite) points on a spheroid or ellipsoid are not identified with each other. They remain separate and in our railway line example would be the 2 intersecting points of the tracks, one in each direction.
Note: Antipodes Island (beside New Zealand) is/was considered to be the anti-podal point of London on the Globe ball, hence the name of the island and the use as a general reference to down-under.
Light is said to be electromagnetic radiation within a certain range of the electromagnetic spectrum. This is called Visible Light, the main source of which is the Sun. Visible light means that the light is visible to the human Eye.
Light is said to be the medium, by which Vision is transported to the Eye. It is said to be both a particle (material) and a wave (immaterial) depending on circumstance and Observation. Light is generally accepted to emanate from all parts of a Luminary (or reflected from an Object that is illuminated) and propagate in all directions in straight lines, as so called Visual Rays that enter the Eye.
Now without Light we have no Vision, since no Object can be seen without Light. Shut your eyes to prove this to yourself. Sight or visual perception then, is the ability to interpret the environment by processing information that is apparently “somehow contained” in visible light.
The interplay between Light and Matter continuously creates visibles, waiting to be seen by the correctly situated optical instrument, such as the Eye. The visibles (figure, extension, color, etc.) keep changing, they neither stop nor start, change is all there is.
Light and visibles seems to live in a different geometric space to our Euclidean world of solid objects. It is a seemingly paradoxical space that co-exists with our tangible world. A kind of dual role is played. It is part of our world, but somehow not a part of it either. It takes up no volume in our local reality and extends in every direction, overlapping and intersecting. In this space two visibles can be in the same place at the same time (e.g. two colors mixing), in direct contrast to a Euclidean space where no two bodies or particles can occupy the same space.
Now, I know that the Objects are still there when I shut my eyes and I bump into them in the dark, so my Euclidean world doesn’t go away when there is no light, only the visual space is gone.
Similarly, I know that visibles exist whether I see them or not. They are created by objects, their environment and illumination, by the colors, the light and shade, etc. and are unique to a particular viewpoint or eye position. They are continuously available for anyone who wants to look. Just as a falling tree will most definitely make a sound in a forest, even when nobody is there to hear it, so will a visible exist, whether somebody is looking or not.
Visibles are a common sense data that we can all share. “Come over here and have look at this”, you say to your friends, when you want to share your view of an object of interest. We have all stopped at viewing places during our travels, to marvel at some spectacular scenery. Whether somebody is looking or not, this visible at this particular viewpoint is a unique, real entity and is independent of the mind. So it seems that:
Visibles are entities of a 2 -Dimensional geometrical space, seen by an optical instrument such as the Eye, of Objects in 3D Euclidean space that are illuminated.
Do individual visibles belong to a set of all possible views, seen from all possible angles, and from all possible Eyes? The visibles change all the time, as the Earth and its animate and inanimate matter “lives and dies” and as we move around and the light changes, etc. Is this set of all possible visibles then finite?
We can never individually experience even a fraction of all the possible visibles, only collectively maybe? Just as we view visibles, so do all other animals, insects and creatures have their view of parts of the total visible space. The plant world (e.g. sunflowers) likewise strive to see the light with their own “eyes” and experience the amazing Light-Matter spectacle of Nature.
Does Light create its own 2D visual geometric space as it propagates? Does it create the visibles in this space as it illuminates? What role does the matter play? Simply that of a reflecting surface? A surface of a physical Object with individual material properties, where reflection is dependent only on the composition of the top few atom layers?
According to modern science, light propagates in straight lines, filling a spherical voulme, with a very fast but finite speed. My experience of light is local and instantaneous. It is obviously a local phenomenon that comes and goes with day and night.
Thought: If a filter could be put directly in front of the Sun that stopped all illumination, and then suddenly pulled away, then I am sure that it would not be dark for 8 minutes until the light reached us ;-) Pity we can’t do that experiment (yet).
It is preposterous to think that Sunlight could come from so far away. Light is said to propagate in all directions as a point source filling a spherical volume as it expands on its way to us. The distance it would expand in reaching us, is the same as the radius of the Earths alleged Orbit round the sun. The Sun to Earth distance is considered to be 109 times the Suns diameter or 218 times its radius. You can fit 218 Suns in the distance between Earth and the Sun. This means that each side of a 1 cm square surface of the Sun, will be 218 cm when it reaches the Earth. So the area is multiplied 218 * 218 times = 47.524 cm squared. The altitude of the visual ray pyramid is the distance from the Earth to the Sun. So the volume of the quadrangular light pyramid (apex at Sun, base on Earth) is 47.524 * 15.000.000.000.000 cm = 712.860.000.000.000.000 cm cubed, and that is only from 1 cm of surface?
What happens to the light? It goes on forever? Never dissipating? What happens to the light when it reaches our eye? Where does it all go? If Light is considered particulate (photon), how the hell can an eye contain and absorb all these particle light rays? What capacity must the eye then have, considering the volume of light reaching it? Hmm..., there is still much said about Light that makes no sense yet.
The geometric space of visibles can be tentatively visualized as a sort of surface, but not one that is part of any 3D Object. I try not to think of artificial Cartesian coordinates and XYZ Axes. It is arranged more in the 2 Dimensions of the natural (cardinal) directions of up/down, left/right.
We do experience an eye shaped spheroidal visual space around us, but this geometrical space should not be directly equated with Spherical Geometry (not even oblate spheroid geometry ;-). It is a useful analog, with many geometrical truths common to both, otherwise ancient navigation and astronomy would not have worked within the error limits that it does, but they are not exactly the same.
The basic axioms of the GOV model, are that of a bi-polar (double) elliptic geometry, the modern name for “spherical geometry”. Bi-polar means that anti-podal (opposite) points on a spheroid or ellipsoid are not identified with each other. They remain separate and in our railway line example would be the 2 intersecting points of the tracks, one in each direction.
Note: Antipodes Island (beside New Zealand) is/was considered to be the anti-podal point of London on the Globe ball, hence the name of the island and the use as a general reference to down-under.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Some Theories of Vision
Here is an example of reading material and references from a modern day course on the Theory of Vision. It lists literature from Philosophy, Psychology, Optic and other associated fields, including critical papers on Reids work.
http://www.socsci.uci.edu/~pjmaddy/bio/vision%20theory%2015-16.pdf
As can be seen from the list, we are a long way from a definitive answer as to how it all works and is a hotly debated subject, even though many would like us to think there is nothing to see here. Move along. It does not seem to be considered in itself worthy of mathematical or physical research but more philosophical and psychological musings.
Here is an example snippet http://hubel.med.harvard.edu/book/b49.htm#con from modern research on the Psychology on Vision which concludes:
“The subject of color vision illustrates so well the possibilities of understanding otherwise quite mysterious phenomena—the results of color mixing or the constancy of colors despite changes in the light source—by using a combination of psychophysical and neurophysiological methods. For all their complexity, the problems presented by color are probably simpler than those presented by form. Despite all the orientation-specific and end stopped cells, we are still a long way from understanding our ability to recognize shapes, to distinguish shapes from their background, or to interpret three dimensions from the flat pictures presented to each of our eyes. To compare the modalities of color and form at all may itself be misleading: remember that differences in color at borders without any differences in luminous intensity, can lead to perception of shapes. Thus color, like black and white, is just one means by which shapes manifest themselves.”
Note the sentence that I underlined, of how little they actually know and the phrase “flat pictures presented to each of our eyes”.
I don’t agree. Pictures are presented to the eye as if on a 2D spherical surface, of which the eye is the center.
Overall, I have yet to read a convincing explanation of how the mind processes the Visual Rays entering our Eye, by some unknown means and properties of Light, and can then "magically" conjure the true Ideas of the Figure, Colour, Magnitude, Situation and Distance of Objects around us. In my opinion, Thomas Reid is the only one who came close.
Now we can certainly engineer optics (glasses, monocles, etc.) and we understand certain parts of the chain, such as the mechanics of Optical instruments or when Biology shows us the component parts of the Eye, such as the lens that focuses the Visual Light Rays onto our curved Retina. Neuroscience talks about neutrons firing in the visual cortex and brain nerves, and they get lights blinking on their “brain measuring” machines, but these are not really explanations of how it works.
Here is an example of reading material and references from a modern day course on the Theory of Vision. It lists literature from Philosophy, Psychology, Optic and other associated fields, including critical papers on Reids work.
http://www.socsci.uci.edu/~pjmaddy/bio/vision%20theory%2015-16.pdf
As can be seen from the list, we are a long way from a definitive answer as to how it all works and is a hotly debated subject, even though many would like us to think there is nothing to see here. Move along. It does not seem to be considered in itself worthy of mathematical or physical research but more philosophical and psychological musings.
Here is an example snippet http://hubel.med.harvard.edu/book/b49.htm#con from modern research on the Psychology on Vision which concludes:
“The subject of color vision illustrates so well the possibilities of understanding otherwise quite mysterious phenomena—the results of color mixing or the constancy of colors despite changes in the light source—by using a combination of psychophysical and neurophysiological methods. For all their complexity, the problems presented by color are probably simpler than those presented by form. Despite all the orientation-specific and end stopped cells, we are still a long way from understanding our ability to recognize shapes, to distinguish shapes from their background, or to interpret three dimensions from the flat pictures presented to each of our eyes. To compare the modalities of color and form at all may itself be misleading: remember that differences in color at borders without any differences in luminous intensity, can lead to perception of shapes. Thus color, like black and white, is just one means by which shapes manifest themselves.”
Note the sentence that I underlined, of how little they actually know and the phrase “flat pictures presented to each of our eyes”.
I don’t agree. Pictures are presented to the eye as if on a 2D spherical surface, of which the eye is the center.
Overall, I have yet to read a convincing explanation of how the mind processes the Visual Rays entering our Eye, by some unknown means and properties of Light, and can then "magically" conjure the true Ideas of the Figure, Colour, Magnitude, Situation and Distance of Objects around us. In my opinion, Thomas Reid is the only one who came close.
Now we can certainly engineer optics (glasses, monocles, etc.) and we understand certain parts of the chain, such as the mechanics of Optical instruments or when Biology shows us the component parts of the Eye, such as the lens that focuses the Visual Light Rays onto our curved Retina. Neuroscience talks about neutrons firing in the visual cortex and brain nerves, and they get lights blinking on their “brain measuring” machines, but these are not really explanations of how it works.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
The Eye
Let’s look at the eye and see what we can agree on.
The Eye is contained in its own socket, is globular and approximately an inch in diameter.
See images on https://en.wikipedia.org/wiki/Retina
Visual Rays (or Vision by means of Light) pass through the Cornea (Horny Coat). They then pass through the Iris, the coloured circle within. An Aperture in the middle lets in the Light or what we call, Vision by means of Light.
Directly behind the Iris, the Visual Rays are focussed by the Crystalline Humour, that functions as a Lens. This is a whitish, strong jelly or cold Glue like substance of moderate consistence. It is as clear and pellucid as Crystal, hence the name. Pellucid means it admits a maximum passage of light without diffusion or distortion; reflecting evenly from all surfaces. Crystal clear. Transparent, clear, bright, glassy.
It is of the same nature and use as a double convex, microscopic Lens and is said to be more convex on one Side (inward towards centre of eye), than the other. Muscular fibres contract or make less convex, the rays of light, by which vision is conveyed, to a Focus beyond this humour in the centre of the eye, so that the images or pictures of objects, can be perfectly rendered depending on whether the objects are closer or farther from the eye. From the centre they diverge and then fall on the bottom or back part of the eye called the retina.
The Aperture or Pupil expands or contracts, when more or less light is needed. It ranges from 3/10 inch in diameter to 1/10 inch and less. This is performed involuntarily, whether we want to or not.
The back part of the eye is lined with a fine membrane of delicate texture, called the retina, from its resemblance of net-work (weaving). The large cavity bounded by the retina and the Crystalline Humour (which is also contained within it), is filled with a glutinous fluid like the white of an egg. Being perfectly pellucid and uncoloured, it is called the vitreous or glassy humour, in which the rays converge, at the centre of the eye. At the centre, the rays contract and cross each other. They then diverge and fall on the retina to form the upside down and left to right Images of objects. This sensation is supposed to be communicated, by the optic nerve to the sensorium of the brain.
Exactly how the rays of light are refracted or otherwise processed when passing through the various humours of the eye seems to be mostly conjectural, from what I can find. Why do I say conjectural?
Well, because we can have perfect vision of an object of any magnitude, through a small pinhole. Try this yourself making a pinhole in cardboard and holding it close to the eye.
You can see large objects just fine although all the light can only be coming in through the small hole. How does the eye do that then if all the rays have to come through that one point?
Let’s look at the eye and see what we can agree on.
The Eye is contained in its own socket, is globular and approximately an inch in diameter.
See images on https://en.wikipedia.org/wiki/Retina
Visual Rays (or Vision by means of Light) pass through the Cornea (Horny Coat). They then pass through the Iris, the coloured circle within. An Aperture in the middle lets in the Light or what we call, Vision by means of Light.
Directly behind the Iris, the Visual Rays are focussed by the Crystalline Humour, that functions as a Lens. This is a whitish, strong jelly or cold Glue like substance of moderate consistence. It is as clear and pellucid as Crystal, hence the name. Pellucid means it admits a maximum passage of light without diffusion or distortion; reflecting evenly from all surfaces. Crystal clear. Transparent, clear, bright, glassy.
It is of the same nature and use as a double convex, microscopic Lens and is said to be more convex on one Side (inward towards centre of eye), than the other. Muscular fibres contract or make less convex, the rays of light, by which vision is conveyed, to a Focus beyond this humour in the centre of the eye, so that the images or pictures of objects, can be perfectly rendered depending on whether the objects are closer or farther from the eye. From the centre they diverge and then fall on the bottom or back part of the eye called the retina.
The Aperture or Pupil expands or contracts, when more or less light is needed. It ranges from 3/10 inch in diameter to 1/10 inch and less. This is performed involuntarily, whether we want to or not.
The back part of the eye is lined with a fine membrane of delicate texture, called the retina, from its resemblance of net-work (weaving). The large cavity bounded by the retina and the Crystalline Humour (which is also contained within it), is filled with a glutinous fluid like the white of an egg. Being perfectly pellucid and uncoloured, it is called the vitreous or glassy humour, in which the rays converge, at the centre of the eye. At the centre, the rays contract and cross each other. They then diverge and fall on the retina to form the upside down and left to right Images of objects. This sensation is supposed to be communicated, by the optic nerve to the sensorium of the brain.
Exactly how the rays of light are refracted or otherwise processed when passing through the various humours of the eye seems to be mostly conjectural, from what I can find. Why do I say conjectural?
Well, because we can have perfect vision of an object of any magnitude, through a small pinhole. Try this yourself making a pinhole in cardboard and holding it close to the eye.
You can see large objects just fine although all the light can only be coming in through the small hole. How does the eye do that then if all the rays have to come through that one point?
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Some Limits of the Eye
Eye vision has certain limits which are important to know.
The total visual field of an eye is said to be 200 degrees left to right. By my own experience I would say about 180, since vision at the boundaries is unclear, without slanting the eyes.
When focussing on an Object (fixation point), in front of you, we only have about 10 – 15 degrees either side of the middle of the Object where vision is really distinct, since your attention is on the object.
You can see on either side, but not distinctly. The further from the center of your focus an object is, the more indistinct is the vision of it.
See the images on https://en.wikipedia.org/wiki/Peripheral_vision
And also https://en.wikipedia.org/wiki/Field_of_view
Your vertical visual field is said to be around 135 degrees (Up and Down), but the comment regarding focus and fixation point made above, also applies.
So the visual field for distinct vision is approximately a circle of 30 degrees around the fixation point. This is referred to as the visual cone, which has its apex at your eye.
Now the limits of distance (backward/forward) is where is gets tricky, since we do not have depth vision, we only have various depth cues, from which we can infer distance based on experience, such as growing up and interacting with tangible space via touch (growing up). These are cues like shading, colours, overlaps, etc. which allow us to better see boundaries and judge distance, but the Eye itself as an optical instrument has no depth in its visual field.
It is said that an Object in the distance can only be seen up-to 3000 or 4000 times its own diameter. So a coin of one-inch diameter, can no longer be seen after about 250 feet. This is assuming “normal conditions”. For a 1 cm diameter coin, this is approximately 30 metres.
However, light can be seen further away, especially in the dark. It is estimated that a 1 mm slit with light shining through it, can be seen up-to 100 metres away. This is a factor of 100.000 times the "height/width" of the slit.
Eye vision has certain limits which are important to know.
The total visual field of an eye is said to be 200 degrees left to right. By my own experience I would say about 180, since vision at the boundaries is unclear, without slanting the eyes.
When focussing on an Object (fixation point), in front of you, we only have about 10 – 15 degrees either side of the middle of the Object where vision is really distinct, since your attention is on the object.
You can see on either side, but not distinctly. The further from the center of your focus an object is, the more indistinct is the vision of it.
See the images on https://en.wikipedia.org/wiki/Peripheral_vision
And also https://en.wikipedia.org/wiki/Field_of_view
Your vertical visual field is said to be around 135 degrees (Up and Down), but the comment regarding focus and fixation point made above, also applies.
So the visual field for distinct vision is approximately a circle of 30 degrees around the fixation point. This is referred to as the visual cone, which has its apex at your eye.
Now the limits of distance (backward/forward) is where is gets tricky, since we do not have depth vision, we only have various depth cues, from which we can infer distance based on experience, such as growing up and interacting with tangible space via touch (growing up). These are cues like shading, colours, overlaps, etc. which allow us to better see boundaries and judge distance, but the Eye itself as an optical instrument has no depth in its visual field.
It is said that an Object in the distance can only be seen up-to 3000 or 4000 times its own diameter. So a coin of one-inch diameter, can no longer be seen after about 250 feet. This is assuming “normal conditions”. For a 1 cm diameter coin, this is approximately 30 metres.
However, light can be seen further away, especially in the dark. It is estimated that a 1 mm slit with light shining through it, can be seen up-to 100 metres away. This is a factor of 100.000 times the "height/width" of the slit.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Visual Appearance and Perspective
Visual Appearance and Perspective
Visual Appearance and Perspective
Perspective is one of the most challenging things to understand, when deciding if you live on a Flat Earth.
Difficulties arise in understanding a setting sun shrinking or sinking, ships disappearing at the horizon, distances and sizes of objects at the horizon or in the sky, railway lines and telegraph poles, etc.
These difficulties often arise due to an incorrect understanding of the origins of perspective and hence its true nature.
The origins of perspective are not in the Art of painting, stage designing or projections onto planes, nor are the roots to be found in mathematical fantasies of higher dimensional geometries.
Perspective is a direct consequence of Optics, from whence the name comes (medieval Latin perspectiva (ars) ‘(science of) optics’)
http://www.etymonline.com/index.php?term=perspective
Direct Vision and Perspective
Perspective is a branch of the science of Optics and Direct Vision Theory that goes back to antiquity.
Direct Vision Theory considers the structure and optics of the human Eye, the geometry of visible light and the nature of vision itself and how it is performed.
It recognizes perspective as an inseparable part of visual experience and not as a modern supplementary artefact of representing objects on planar surfaces to produce images or pictures.
Here are some sources and quotes on the roots of perspective before we dive deeper.
http://www.dartmouth.edu/~matc/math5.geometry/unit11/unit11.html
“Like most discoveries, perspective theory did not emerge out of a vacuum. The underlying ideas had been accumulating for centuries. While the main application of perspective is in art, it is an optical phenomenon and thus has its principal root not in art but in geometrical optics.”
“Vitruvius (ca. 50 BC) wrote: Perspective is the method of sketching a front with the sides withdrawing into the background, the lines all meeting in the center of a circle”.
Unfortunately, he didn't elaborate on that, but we will.
“Ptolemy's Optica, c. 140 A.D., was another early text on geometrical optics, and included theories on refraction. The centric ray is defined by Ptolemy as the ray that does not get refracted. The centric ray, we'll see, is important in the theory of perspective. In his Geographia, c. 140 A.D., Ptolemy applies the principles of geometric optics to the projection of the spherical surface of the earth onto a flat surface, to produce a map. He is said to have made the first known linear perspective construction for drawing a map of the world. Ptolemy apparently knew about perspective, but applied it only to maps and to stage designs.”
Here we can already see the beginnings of the role played by geometric optics in the space ball deception.
Piero della Francesca (ca. 1450)
https://en.wikipedia.org/wiki/Piero_della_Francesca
“First is sight, that is to say the eye; second is the form of the thing seen; third is the distance from the eye to the thing seen; fourth are the lines which leave the boundaries of the object and come to the eye; fifth is the intersection, which comes between the eye and the thing seen, and on which it is intended to record the object. “
Here we can (still) see the dependency of perspective on the Eye and the Object as prerequisites for perspective.
EUCLID (ca. 300 BC)
I think one of the most important missing pieces of the puzzle is the little known treatise called Euclid’s OPTICS
We all know EUCLID. The validity of his volume ELEMENTS is proven daily in all aspects of mathematics, engineering, construction, etc.
As mathematicians say “IF Euclidean geometry falls, it ALL falls”, although that didn’t stop them wanking over hyperbolic geometry.
Don’t worry, nothing falls. Euclid already had part of the answer. His treatise OPTICS (together with Sphaerica) is the foundations for the geometry of navigation, astronomy and the celestial sphere, although it would seem to have been well hidden for thousands of years.
Why do I say hidden? Well the first English translation of OPTICS was in 1945. Until then there was only ancient Greek, Latin and Arabic translations for thousands of years. Or did I miss that memo?
Get it and READ it here. https://archive.org/details/TheOpticsOfEuclid
(see the footnote on page 1)
We will look later in more detail at the most relevant propositions and how they impact our understanding of perspective.
VISUAL APPEARANCES
Euclid’s OPTICS contains propositions and theories of VISION and APPEARANCES.
From the page Ancient vision:
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/AncientVisions.htm
“Euclid's contribution to vision (the "Optica") was actually a theory of light, not vision. Though he adopted the extramission theory to the extent that he maintained that "visual rays" exit forth from the eyes, this was not vital to the theory, which was essentially a system of mathematics, concerned with the geometrical properties of light rays. This theory formed the basis of navigation methods, of perspective and of astronomy, for more than two millenia, and is still essentially valid today.”
At the start of OPTICS, some important definitions are introduced for the first time, such as the concept of a visual cone and visual rays.
Light travels in straight lines and is supposed to convey vision by some still unknown and unexplained means. Light rays are said to extend from objects in all directions. A visual ray is a straight line from the point on an object to the centre of your eye.
A visual cone has its apex at the centre of your Eye. The circular base is the surface of vision, through which visual rays must pass, and whose area covers the objects being viewed and whose perimeter relates to specific limits on distinctness of vision, depending on a given situation.
Note that it does not matter whether you believe in Extramission (rays proceed from eye to object) or Intramission (rays proceed from object to eye), or a combination of both. The geometry of the basic line is reversible. It simply connects two points and we are not concerned at this stage with direction.
“The commonest interpretation of light and vision in classical times was in terms of straight rays from the eye and from sources of light. A ray from the sun would illuminate an object, and make it visible when touched by a ray from the eye. Epicureans, however, held that light was a subtle substance emitted from sources of light that was reflected by an object to enter the eye, producing the sensation of vision. The latter view is, of course, closer to the modern one, but there was then no way to verify one view or the other, so the simpler, and wrong, one was chosen“.
The concept of straight visual rays is fundamental to OPTICS and confirmed by engineering and experience. The principle is easily seen in the workings of a pinhole camera or Camera Obscura, where inverted images of objects are formed, when light shines through a small aperture.
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/ExperimentsWithCameraObscura.htm
Here are some more links to historical accounts regarding vision
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/
Here some of the dabbling done by Kepler & Co.
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/InvertedRetinalImage.htm
APPEARANCES vs REPRESENTATION
Understanding Direct Vision is to distinguish between the REPRESENTATION of objects on a PLANE, and their real or true APPEARANCE to the EYE.
REPRESENTATION on a PLANE and APPEARANCE to the EYE are NOT the same thing.
APPEARANCE depends only on the relations of TWO things to each other, namely the OBJECT and the EYE.
REPRESENTATION depends on the relations of THREE things to each other. The same two as above and additionally the PLANE (or in general the surface of projection).
REPRESENTATION is therefore only a relative appearance that depends on the particular situation of all three things together, the Eye, Object and Plane.
APPEARANCE is the true view by the EYE and is embedded in our natural sensorium.
We didn’t/don’t realise this difference nor imagine a distinction to exist, but it is key to understanding the major philosophical debate on the nature of vision, unanswered to this day, and will help discard the space ball conditioning we have been subjected to.
One-eyed symbolism is a meme for, and a mockery of, the sheeple who have their eye covered with the flat palm of a hand. I think it is a reference to the perspective plane that has been put in front of our eyes, via shadows on walls, canvas, paper, stage, TV, computers and now smartphones.
We no longer attend to what we truly see, but to images and pictures represented to us on a PLANE.
The deception itself is, as they say, “hidden in PLANE sight”.
APPEARANCES ARE EVERYTHING
Contrary to the deliberately propagated meme “appearances mean nothing”, the opposite is actually true.
The APPEARANCE of Objects or its constituent parts, means “the angle subtended at the eye” by the visual rays connecting the points on the object to the Eye. It is the angle formed by two rays at the Eye.
The DISAPPEARANCE of an Object means that the angle subtended at the Eye is so small (1/60 of a degree or 1 minute of space) as to be indistinguishable.
APPEARANCES are formed when we AIM. A visible figure is seen when our feet point forward, and our nose follows our eyes with a pointing finger to an object in a direct Line of Sight. Objects then APPEAR in our vision.
Visual APPEARANCES are used to determine Magnitudes and Bearings of Objects with respect to each other. To “bear witness” is to confirm the visual appearance seen by somebody else.
Straight line visual rays from the object(s) to the eye, intercept the visual cone (or spherical sector), that is centred at the Eye. These interception points form portions of an ARC of a circle. To determine relationships between objects, or between constituent parts of objects we use the following:
The ratios of the arc segment lengths, determine the proportions of the Objects to each other and are the same ratios as the angles subtended at the Eye.
These relationships are quantified in dimensionless units called Radians for 2D planar angles or Steradians (square radians) for solid angles in 3-D spherical geometry. Note that “radius” is Latin for “rays” or “beams”. In both cases the measure is related to the radius of the circle or of the sphere.
https://en.wikipedia.org/wiki/Radian
https://en.wikipedia.org/wiki/Steradian
https://en.wikipedia.org/wiki/Arc_(geometry)
A better way to think of this uses the concept of “Spread” (angles) and “Quadrature” (areas), from rational geometry, but we won’t go there at the moment.
Note that we are not using a coordinate system, only considering ratios of qualities of objects to each other.
REPRESENTATION on a PLANE
PROJECTION is the Transcription or Delineation of an Object upon a PLANE to create a REPRESENTATION of the object as a picture or image.
It is the Figure marked or traced upon a plane (more generally any surface), by a moveable line, extended from the EYE, as a common Pole or Centre to the several Points of an Object.
It is sometimes called a SECTION, because the Figure or Image, or REPRESENTATION of the Object on the Plane (which process we call PROJECTION), is the SECTION of the Visual Cone, Pyramid, Cylinder or Prism made by the Plane on which the said Figure is imaged or pictured.
A great variety of projections arise, from the various positions of the Eye, the visible Object and the Plane itself. In addition to this well-known linear perspective, there is also cylindrical perspective and spherical perspective, but more of that later.
An important distinction between the PROJECTION and the bare APPEARANCE of an Object to the Eye is the following:
If the Eye and the Object retain their positions, the APPEARANCE will always be the same, even if the position of the Plane is changed, but the REPRESENTATION on the Plane will not be the same, it can be very different.
It is this added consideration of a plane, that distinguishes the science of PROJECTION, from DIRECT OPTICS.
In OPTICS we consider Quantities purely as VISIBLE, or as the Objects of Vision, whereas in a PROJECTION they are considered as visible REPRESENTATIONS with respect to a certain plane, situated in a particular position.
Summary
I once read a Youtube comment: “The maths for the globe must be based on the laws of perspective for flat earth to make sense.”
This is nearly an accurate summary of the situation/problem, except it is not the laws of perspective but more correctly the maths for Optics and Visual Appearances, that is the basis geometry for perspective, astronomy, navigation, celestial sphere, spherical geometry (non-euclidean), projective geometry and curvature of surfaces.
It is the reason the "dual mathematics" (aka George Orwell 1984) works, and how it goes/went unnoticed for so long.
Perspective is one of the most challenging things to understand, when deciding if you live on a Flat Earth.
Difficulties arise in understanding a setting sun shrinking or sinking, ships disappearing at the horizon, distances and sizes of objects at the horizon or in the sky, railway lines and telegraph poles, etc.
These difficulties often arise due to an incorrect understanding of the origins of perspective and hence its true nature.
The origins of perspective are not in the Art of painting, stage designing or projections onto planes, nor are the roots to be found in mathematical fantasies of higher dimensional geometries.
Perspective is a direct consequence of Optics, from whence the name comes (medieval Latin perspectiva (ars) ‘(science of) optics’)
http://www.etymonline.com/index.php?term=perspective
Direct Vision and Perspective
Perspective is a branch of the science of Optics and Direct Vision Theory that goes back to antiquity.
Direct Vision Theory considers the structure and optics of the human Eye, the geometry of visible light and the nature of vision itself and how it is performed.
It recognizes perspective as an inseparable part of visual experience and not as a modern supplementary artefact of representing objects on planar surfaces to produce images or pictures.
Here are some sources and quotes on the roots of perspective before we dive deeper.
http://www.dartmouth.edu/~matc/math5.geometry/unit11/unit11.html
“Like most discoveries, perspective theory did not emerge out of a vacuum. The underlying ideas had been accumulating for centuries. While the main application of perspective is in art, it is an optical phenomenon and thus has its principal root not in art but in geometrical optics.”
“Vitruvius (ca. 50 BC) wrote: Perspective is the method of sketching a front with the sides withdrawing into the background, the lines all meeting in the center of a circle”.
Unfortunately, he didn't elaborate on that, but we will.
“Ptolemy's Optica, c. 140 A.D., was another early text on geometrical optics, and included theories on refraction. The centric ray is defined by Ptolemy as the ray that does not get refracted. The centric ray, we'll see, is important in the theory of perspective. In his Geographia, c. 140 A.D., Ptolemy applies the principles of geometric optics to the projection of the spherical surface of the earth onto a flat surface, to produce a map. He is said to have made the first known linear perspective construction for drawing a map of the world. Ptolemy apparently knew about perspective, but applied it only to maps and to stage designs.”
Here we can already see the beginnings of the role played by geometric optics in the space ball deception.
Piero della Francesca (ca. 1450)
https://en.wikipedia.org/wiki/Piero_della_Francesca
“First is sight, that is to say the eye; second is the form of the thing seen; third is the distance from the eye to the thing seen; fourth are the lines which leave the boundaries of the object and come to the eye; fifth is the intersection, which comes between the eye and the thing seen, and on which it is intended to record the object. “
Here we can (still) see the dependency of perspective on the Eye and the Object as prerequisites for perspective.
EUCLID (ca. 300 BC)
I think one of the most important missing pieces of the puzzle is the little known treatise called Euclid’s OPTICS
We all know EUCLID. The validity of his volume ELEMENTS is proven daily in all aspects of mathematics, engineering, construction, etc.
As mathematicians say “IF Euclidean geometry falls, it ALL falls”, although that didn’t stop them wanking over hyperbolic geometry.
Don’t worry, nothing falls. Euclid already had part of the answer. His treatise OPTICS (together with Sphaerica) is the foundations for the geometry of navigation, astronomy and the celestial sphere, although it would seem to have been well hidden for thousands of years.
Why do I say hidden? Well the first English translation of OPTICS was in 1945. Until then there was only ancient Greek, Latin and Arabic translations for thousands of years. Or did I miss that memo?
Get it and READ it here. https://archive.org/details/TheOpticsOfEuclid
(see the footnote on page 1)
We will look later in more detail at the most relevant propositions and how they impact our understanding of perspective.
VISUAL APPEARANCES
Euclid’s OPTICS contains propositions and theories of VISION and APPEARANCES.
From the page Ancient vision:
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/AncientVisions.htm
“Euclid's contribution to vision (the "Optica") was actually a theory of light, not vision. Though he adopted the extramission theory to the extent that he maintained that "visual rays" exit forth from the eyes, this was not vital to the theory, which was essentially a system of mathematics, concerned with the geometrical properties of light rays. This theory formed the basis of navigation methods, of perspective and of astronomy, for more than two millenia, and is still essentially valid today.”
At the start of OPTICS, some important definitions are introduced for the first time, such as the concept of a visual cone and visual rays.
Light travels in straight lines and is supposed to convey vision by some still unknown and unexplained means. Light rays are said to extend from objects in all directions. A visual ray is a straight line from the point on an object to the centre of your eye.
A visual cone has its apex at the centre of your Eye. The circular base is the surface of vision, through which visual rays must pass, and whose area covers the objects being viewed and whose perimeter relates to specific limits on distinctness of vision, depending on a given situation.
Note that it does not matter whether you believe in Extramission (rays proceed from eye to object) or Intramission (rays proceed from object to eye), or a combination of both. The geometry of the basic line is reversible. It simply connects two points and we are not concerned at this stage with direction.
“The commonest interpretation of light and vision in classical times was in terms of straight rays from the eye and from sources of light. A ray from the sun would illuminate an object, and make it visible when touched by a ray from the eye. Epicureans, however, held that light was a subtle substance emitted from sources of light that was reflected by an object to enter the eye, producing the sensation of vision. The latter view is, of course, closer to the modern one, but there was then no way to verify one view or the other, so the simpler, and wrong, one was chosen“.
The concept of straight visual rays is fundamental to OPTICS and confirmed by engineering and experience. The principle is easily seen in the workings of a pinhole camera or Camera Obscura, where inverted images of objects are formed, when light shines through a small aperture.
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/ExperimentsWithCameraObscura.htm
Here are some more links to historical accounts regarding vision
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/
Here some of the dabbling done by Kepler & Co.
http://nivea.psycho.univ-paris5.fr/FeelingSupplements/InvertedRetinalImage.htm
APPEARANCES vs REPRESENTATION
Understanding Direct Vision is to distinguish between the REPRESENTATION of objects on a PLANE, and their real or true APPEARANCE to the EYE.
REPRESENTATION on a PLANE and APPEARANCE to the EYE are NOT the same thing.
APPEARANCE depends only on the relations of TWO things to each other, namely the OBJECT and the EYE.
REPRESENTATION depends on the relations of THREE things to each other. The same two as above and additionally the PLANE (or in general the surface of projection).
REPRESENTATION is therefore only a relative appearance that depends on the particular situation of all three things together, the Eye, Object and Plane.
APPEARANCE is the true view by the EYE and is embedded in our natural sensorium.
We didn’t/don’t realise this difference nor imagine a distinction to exist, but it is key to understanding the major philosophical debate on the nature of vision, unanswered to this day, and will help discard the space ball conditioning we have been subjected to.
One-eyed symbolism is a meme for, and a mockery of, the sheeple who have their eye covered with the flat palm of a hand. I think it is a reference to the perspective plane that has been put in front of our eyes, via shadows on walls, canvas, paper, stage, TV, computers and now smartphones.
We no longer attend to what we truly see, but to images and pictures represented to us on a PLANE.
The deception itself is, as they say, “hidden in PLANE sight”.
APPEARANCES ARE EVERYTHING
Contrary to the deliberately propagated meme “appearances mean nothing”, the opposite is actually true.
The APPEARANCE of Objects or its constituent parts, means “the angle subtended at the eye” by the visual rays connecting the points on the object to the Eye. It is the angle formed by two rays at the Eye.
The DISAPPEARANCE of an Object means that the angle subtended at the Eye is so small (1/60 of a degree or 1 minute of space) as to be indistinguishable.
APPEARANCES are formed when we AIM. A visible figure is seen when our feet point forward, and our nose follows our eyes with a pointing finger to an object in a direct Line of Sight. Objects then APPEAR in our vision.
Visual APPEARANCES are used to determine Magnitudes and Bearings of Objects with respect to each other. To “bear witness” is to confirm the visual appearance seen by somebody else.
Straight line visual rays from the object(s) to the eye, intercept the visual cone (or spherical sector), that is centred at the Eye. These interception points form portions of an ARC of a circle. To determine relationships between objects, or between constituent parts of objects we use the following:
The ratios of the arc segment lengths, determine the proportions of the Objects to each other and are the same ratios as the angles subtended at the Eye.
These relationships are quantified in dimensionless units called Radians for 2D planar angles or Steradians (square radians) for solid angles in 3-D spherical geometry. Note that “radius” is Latin for “rays” or “beams”. In both cases the measure is related to the radius of the circle or of the sphere.
https://en.wikipedia.org/wiki/Radian
https://en.wikipedia.org/wiki/Steradian
https://en.wikipedia.org/wiki/Arc_(geometry)
A better way to think of this uses the concept of “Spread” (angles) and “Quadrature” (areas), from rational geometry, but we won’t go there at the moment.
Note that we are not using a coordinate system, only considering ratios of qualities of objects to each other.
REPRESENTATION on a PLANE
PROJECTION is the Transcription or Delineation of an Object upon a PLANE to create a REPRESENTATION of the object as a picture or image.
It is the Figure marked or traced upon a plane (more generally any surface), by a moveable line, extended from the EYE, as a common Pole or Centre to the several Points of an Object.
It is sometimes called a SECTION, because the Figure or Image, or REPRESENTATION of the Object on the Plane (which process we call PROJECTION), is the SECTION of the Visual Cone, Pyramid, Cylinder or Prism made by the Plane on which the said Figure is imaged or pictured.
A great variety of projections arise, from the various positions of the Eye, the visible Object and the Plane itself. In addition to this well-known linear perspective, there is also cylindrical perspective and spherical perspective, but more of that later.
An important distinction between the PROJECTION and the bare APPEARANCE of an Object to the Eye is the following:
If the Eye and the Object retain their positions, the APPEARANCE will always be the same, even if the position of the Plane is changed, but the REPRESENTATION on the Plane will not be the same, it can be very different.
It is this added consideration of a plane, that distinguishes the science of PROJECTION, from DIRECT OPTICS.
In OPTICS we consider Quantities purely as VISIBLE, or as the Objects of Vision, whereas in a PROJECTION they are considered as visible REPRESENTATIONS with respect to a certain plane, situated in a particular position.
Summary
I once read a Youtube comment: “The maths for the globe must be based on the laws of perspective for flat earth to make sense.”
This is nearly an accurate summary of the situation/problem, except it is not the laws of perspective but more correctly the maths for Optics and Visual Appearances, that is the basis geometry for perspective, astronomy, navigation, celestial sphere, spherical geometry (non-euclidean), projective geometry and curvature of surfaces.
It is the reason the "dual mathematics" (aka George Orwell 1984) works, and how it goes/went unnoticed for so long.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
This video seems fitting for this thread:
and Part 2:
and Part 2:

csp- Posts : 424
Points : 4726
Reputation : 1054
Join date : 2016-01-04
Location : Australia
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
vortexpuppy wrote:One-eyed symbolism is a meme for, and a mockery of, the sheeple who have their eye covered with the flat palm of a hand. I think it is a reference to the perspective plane that has been put in front of our eyes, via shadows on walls, canvas, paper, stage, TV, computers and now smartphones.
We no longer attend to what we truly see, but to images and pictures represented to us on a PLANE.
The deception itself is, as they say, “hidden in PLANE sight”.
So the sneaky bastards have taken the curve out of our eye and told us we live on a ball and clouded the issue even more with the Perspective stuff.

vortexkitten- Posts : 37
Points : 3375
Reputation : 87
Join date : 2015-12-31
Forest4theTreez likes this post
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
[quote="csp"]This video seems fitting for this thread:
Hi CSP, Yes fits well. Will take a look thanks.
Hi CSP, Yes fits well. Will take a look thanks.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.

From NASA : https://en.wikipedia.org/wiki/File:Einstein_gyro_gravity_probe_b.jpg
In your face and plane as day.
They are mockingly demonstrating true APPEARANCES and the spherical geometry of vision.
We get fed on planar representations called pictures. Projections on flat screens like shadows on the wall.
Looking through the hemispherical retina, with your eye at the center of the sphere or hemisphere, is geometrically equivalent to the vision on your retina (the images inscribed onto your retina by light), in the sense that the angles (of Objects) subtended at the eye, keep the same ratios to each other, as they do when seen on the curved surface held in front of your eye.
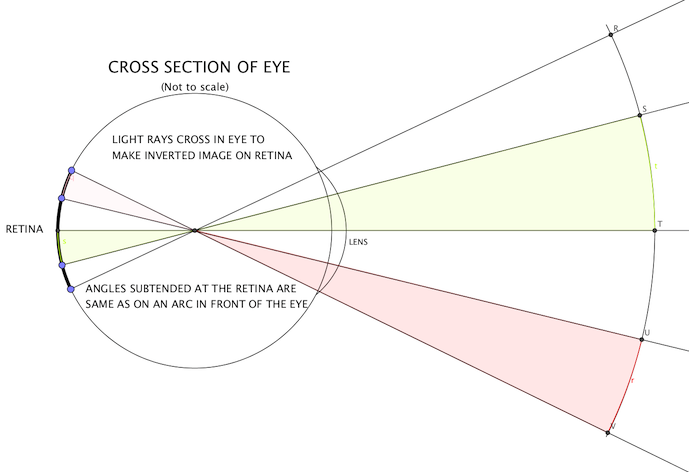
Images on the surface of a sphere are described by spherical geometry, the concept of a 2D curved surface (sphere) embedded in 3D space (on a ball).
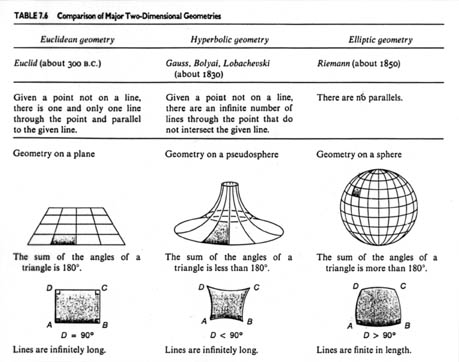
The plane is our reality, the spherical geometry is in the eye.
The pseudosphere is representative of the visual cone and interestingly has the same Gaussian curvature as the sphere only negative.
G of Pseudosphere = -1/R(squared) and the G of Sphere = 1/R(squared)
The good news is that Flat Earth Geometry and Math work just fine for navigation, astronomy, curvature and perspective.
In fact, they've already done the work for us when we adopt the model as the geometry of vision with the Eye at the center of the sphere.

Ignore the ball in the middle of the figure and think only of your Eye placed at the origin of a hemisphere.
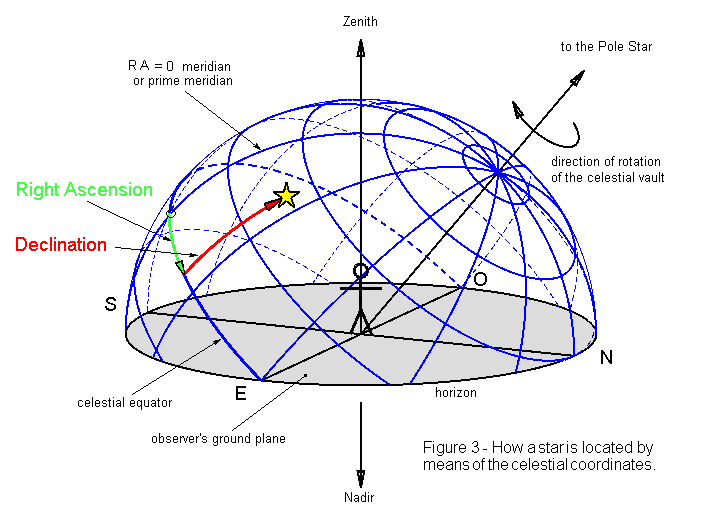
Last edited by vortexpuppy on Thu Jul 14, 2016 1:31 pm; edited 1 time in total
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
vortexpuppy wrote:This video seems fitting for this thread:
Hi CSP, Yes fits well. Will take a look thanks.
I see also other YT channels approaching the subject via angular resolution (e.g. Brian Mullin, Red Pill) and limits of the eye.
IMHO, they still need to differentiate REPRESENTATION and APPEARANCE and factor spherical geometry.
I also see that globehead shills (e.g. fiveredpears) are out in force, trying to catch the flat earth lunatics with their butterfly nets. lol.
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
This thread and its contents are absolutely AMAZING, vortexpuppy. WOW. This confirms the intuition I've had for YEARS regarding "being taught how to see reality wrong". This is explained wonderfully. I'm looking more into those resources you've mentioned above.
Thank you for this incredibly invaluable resource.
Thank you for this incredibly invaluable resource.
Occamania- Posts : 4
Points : 3074
Reputation : 9
Join date : 2016-07-07
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
Direct Vision Limits:
The eye is at E, which is the centre of the arc UN. The altitude or height of the eye at E, is 2 units. IG and HF are parallel lines. IG is at a height (or altitude) of 6 units. HF is at ground or sea level.
The objects HI, AB, CD and FG, each have a vertical diameter or height of 6 units. They are placed parallel to each other and perpendicular to the ground plane and the Eye-Line. The interval spacing between the objects is 6 units, a ratio of 3 to the height of the eye.
Visual rays connect the objects extremes (the top points I, B, D and G, and the bottom points H, A, C and F) to the eye, as shown by the lines EI, EH, EB, EA, EC, ED, EF and EG.
The ratio of the angles to each other, that are made on the arc UN by the visual rays cutting its surface, are in the same ratios as the angles subtended at the eye, on its curved retina.
The top interval (spacing) IB, will appear to move from N to O on the arc, whilst the corresponding bottom interval HA, will move from U to T on the arc. The top interval BD, will appear to move from O to P on the arc, whilst the bottom interval AC, will move from T to S on the arc. So with increased distance, the top line IG, will continually sink on the arc, just as the bottom line HF will continually rise. They both tend to the Eye-Line when extended indefinitely.
The arc length NO is obviously larger than UT, and OP is obviously larger than TS, and so the angles they subtend at the eye are also larger. Now objects appear to have that proportion to each other, respectively, as the angles under which they are seen. So we obviously see more of the top part of the object, that part which is above the Eye- Line, than we do of the bottom part.
When the object is even farther distanced from the eye, as in going from C to F, then the bottom interval will move from S to R on the arc. The angle becomes ever smaller and the point on the arc moves ever closer to the point where the Eye-Line intersects the arc.
When this angle (e.g. arc length SR) is less than 1 minute (1/60th of a degree = 0.0167 degrees), then any ground intervals, an equal interval spacing of 2 units, that are even farther distanced from the Eye, are no longer distinguishable from one another. There is then no distinct, discernible division between the previous interval or the consecutive interval. The surface areas of all these indistinct intervals are condensed into an ever smaller visual angle that eventually disappears from sight.

So when do the bottoms extremes of the objects vanish from sight?
When that distance is reached, where the interval spacing between the bottoms of consecutive objects, subtends an angle at the eye, that is less than 1/60th of a degree or 1 arc minute, an average angular minimum for distinct vision.
For example, when the angle between EC and EF is less than 0.0167 degrees, or the arc length SR, is less than one arc minute, then the interval CF will no longer be seen.
Or when the angle made between ER and the Eye-Line is less than 0.0167 degrees, or its arc length (the point where the Eye-Line intersects the arc is not drawn), is less than one arc minute, then any object contained within that interval will no longer be seen.
The 1 arc minute limit, to see a 2m sized object (1:1 ratio to eye level height) is reached at approximately 6900 meters. This is a 3450:1 ratio of distance to the object diameter. So when the object is at a distance that is 3450 times its own diameter, then the bottom will no longer be distinctly seen. The definition of the "bottom part" of an object depends on the ratio of the objects divisions or its component parts.

Imagine the object is a multi-floor building APPEARING smaller as you DISTANCE yourself. If each floor/story is 4m high, then the ground floor goes from 0 to 4m and the 1st floor goes from 4 to 8m, etc.
Suppose the Ground floor had a line drawn across it at the height of 2m, bisecting the ground floor height (4m) into 2 equal halves, from 0 to 2m and 2 to 4m, from the ground. This line is at the same altitude as the eye.
At approximately 7 km, the limit of vision is reached, so that the two halves of the ground floor will not be distinguishable from each other. The line in the middle will not be seen. The ground floor will lose its form and blur. Eventually the whole ground floor will vanish, when again the angle subtended at the eye, by its top and bottom extremes, reaches the visual limit.
Note: The theoretical physical diffraction limit is smaller, but no optical instrument reaches this. It is impossible to "zoom-in" indefinitely.
Note: Farther removed from the eye = Left/Right or Up/Down. Farther distanced from the eye = Forward/Backward.
The eye is at E, which is the centre of the arc UN. The altitude or height of the eye at E, is 2 units. IG and HF are parallel lines. IG is at a height (or altitude) of 6 units. HF is at ground or sea level.

The objects HI, AB, CD and FG, each have a vertical diameter or height of 6 units. They are placed parallel to each other and perpendicular to the ground plane and the Eye-Line. The interval spacing between the objects is 6 units, a ratio of 3 to the height of the eye.
Visual rays connect the objects extremes (the top points I, B, D and G, and the bottom points H, A, C and F) to the eye, as shown by the lines EI, EH, EB, EA, EC, ED, EF and EG.
The ratio of the angles to each other, that are made on the arc UN by the visual rays cutting its surface, are in the same ratios as the angles subtended at the eye, on its curved retina.
The top interval (spacing) IB, will appear to move from N to O on the arc, whilst the corresponding bottom interval HA, will move from U to T on the arc. The top interval BD, will appear to move from O to P on the arc, whilst the bottom interval AC, will move from T to S on the arc. So with increased distance, the top line IG, will continually sink on the arc, just as the bottom line HF will continually rise. They both tend to the Eye-Line when extended indefinitely.
The arc length NO is obviously larger than UT, and OP is obviously larger than TS, and so the angles they subtend at the eye are also larger. Now objects appear to have that proportion to each other, respectively, as the angles under which they are seen. So we obviously see more of the top part of the object, that part which is above the Eye- Line, than we do of the bottom part.
When the object is even farther distanced from the eye, as in going from C to F, then the bottom interval will move from S to R on the arc. The angle becomes ever smaller and the point on the arc moves ever closer to the point where the Eye-Line intersects the arc.
When this angle (e.g. arc length SR) is less than 1 minute (1/60th of a degree = 0.0167 degrees), then any ground intervals, an equal interval spacing of 2 units, that are even farther distanced from the Eye, are no longer distinguishable from one another. There is then no distinct, discernible division between the previous interval or the consecutive interval. The surface areas of all these indistinct intervals are condensed into an ever smaller visual angle that eventually disappears from sight.

So when do the bottoms extremes of the objects vanish from sight?
When that distance is reached, where the interval spacing between the bottoms of consecutive objects, subtends an angle at the eye, that is less than 1/60th of a degree or 1 arc minute, an average angular minimum for distinct vision.
For example, when the angle between EC and EF is less than 0.0167 degrees, or the arc length SR, is less than one arc minute, then the interval CF will no longer be seen.
Or when the angle made between ER and the Eye-Line is less than 0.0167 degrees, or its arc length (the point where the Eye-Line intersects the arc is not drawn), is less than one arc minute, then any object contained within that interval will no longer be seen.
The 1 arc minute limit, to see a 2m sized object (1:1 ratio to eye level height) is reached at approximately 6900 meters. This is a 3450:1 ratio of distance to the object diameter. So when the object is at a distance that is 3450 times its own diameter, then the bottom will no longer be distinctly seen. The definition of the "bottom part" of an object depends on the ratio of the objects divisions or its component parts.

Imagine the object is a multi-floor building APPEARING smaller as you DISTANCE yourself. If each floor/story is 4m high, then the ground floor goes from 0 to 4m and the 1st floor goes from 4 to 8m, etc.
Suppose the Ground floor had a line drawn across it at the height of 2m, bisecting the ground floor height (4m) into 2 equal halves, from 0 to 2m and 2 to 4m, from the ground. This line is at the same altitude as the eye.
At approximately 7 km, the limit of vision is reached, so that the two halves of the ground floor will not be distinguishable from each other. The line in the middle will not be seen. The ground floor will lose its form and blur. Eventually the whole ground floor will vanish, when again the angle subtended at the eye, by its top and bottom extremes, reaches the visual limit.
Note: The theoretical physical diffraction limit is smaller, but no optical instrument reaches this. It is impossible to "zoom-in" indefinitely.
Note: Farther removed from the eye = Left/Right or Up/Down. Farther distanced from the eye = Forward/Backward.
Last edited by vortexpuppy on Mon Jul 25, 2016 3:43 pm; edited 1 time in total (Reason for editing : Removed paragraph that was relevant to another problem and got mixed up here.)
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
 Re: Direct Vision, Rationality, Realism and Common Sense.
Re: Direct Vision, Rationality, Realism and Common Sense.
The above methods can be applied to explain the visual perspective we experience of:
1) Ships DISAPPEARING over the fantasy curve, "hull first, mast last".
2) Buildings DISAPPEARING out of sight, "bottoms up"
3) The sun sinking below the horizon. It is best to imagine a "+" drawn in the sun disc, connecting horizontal and vertical diameters.
When the altitude of the eye is higher, more of the object(s) and/or their constituent parts will be seen longer, since the visual angle is bigger.
So run up a hill or the Burj Khalifa, to see the sun setting again :-)
I will create individual diagrams for these scenarios to make the principles more clear...
1) Ships DISAPPEARING over the fantasy curve, "hull first, mast last".
2) Buildings DISAPPEARING out of sight, "bottoms up"
3) The sun sinking below the horizon. It is best to imagine a "+" drawn in the sun disc, connecting horizontal and vertical diameters.
When the altitude of the eye is higher, more of the object(s) and/or their constituent parts will be seen longer, since the visual angle is bigger.
So run up a hill or the Burj Khalifa, to see the sun setting again :-)
I will create individual diagrams for these scenarios to make the principles more clear...
Last edited by vortexpuppy on Mon Jul 25, 2016 3:59 pm; edited 2 times in total (Reason for editing : Removed paragraph that was relevant to another problem and got mixed up here.)
vortexpuppy- Posts : 167
Points : 3721
Reputation : 296
Join date : 2015-12-30
Page 1 of 5 • 1, 2, 3, 4, 5 
 Similar topics
Similar topics» CoronaVirus and Forced Vaccination Manipulation
» CoronaVirus and Forced Vaccination Manipulation
» No Curvature on the Flat Earth
» Devin Madgy and Quasiluminous Blood Over Intent Non-Sense
» World Space Agencies
» CoronaVirus and Forced Vaccination Manipulation
» No Curvature on the Flat Earth
» Devin Madgy and Quasiluminous Blood Over Intent Non-Sense
» World Space Agencies
IFERS - Exposing the 'Global' Conspiracy From Atlantis to Zion :: The International Flat Earth Research Society
Page 1 of 5
Permissions in this forum:
You cannot reply to topics in this forum